
已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题:
①若l?α,m?α,l∥β,m∥β,则α∥β;
②若l?α,l∥β,α∩β=m,则l∥m;
③若α∥β,l∥α则l∥β;
④若l⊥α,m∥l,α∥β,则m⊥β.
其中真命题是______________(写出所有真命题的序号).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则 (写出所有正确结论的编号).
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,直线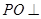 平面
平面 ,垂足为
,垂足为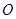 ,直线
,直线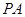 是平面
是平面 的一条斜线,斜足为
的一条斜线,斜足为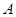 ,其中
,其中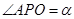 ,过点
,过点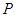 的动直线
的动直线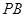 交平面
交平面 于点
于点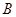 ,
,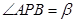 ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①若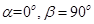 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;
②若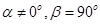 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;
③若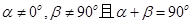 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;
④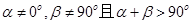 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;
⑤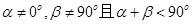 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知α、β、γ是三个不同的平面,命题“α∥β,且α⊥γ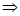 β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题: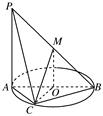
①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;④平面PAC⊥平面PBC.
其中正确的命题是________(填上所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在正三棱锥P ABC中,D,E分别是AB,BC的中点,下列结论:①AC⊥PB;②AC∥平面PDE;③AB⊥平面PDE,其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题:①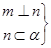 ⇒m⊥α;②
⇒m⊥α;②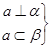 ⇒α⊥β;
⇒α⊥β;
③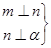 ⇒m∥n;④
⇒m∥n;④ ⇒m∥n
⇒m∥n
其中为真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.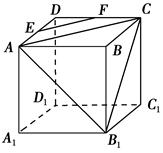
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.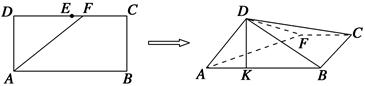
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com