练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知α，β是两个不同的平面，给出下列四个条件：
    ①存在一条直线a，a⊥α，a⊥β；
    ②存在一个平面γ，γ⊥α，γ⊥β；
    ③存在两条平行直线a，b，a?α，b?β，a∥β，b∥α；
    ④存在两条异面直线a，b，a?α，b?β，a∥β，b∥α.
    可以推出α∥β的是(　　)

    A．①③ B．②④ C．①④ D．②③

    C

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    如图，在直四棱柱中，底面ABCD为等腰梯形，AB∥CD,AB="4,BC=CD=2," AA="2, " E、E、F分别是棱AD、AA、AB的中点。               
    （Ⅰ）证明：直线∥平面；w.w.w.k.s.5.u.c.o.m          
    （Ⅱ）求二面角的余弦值

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在△ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，则P到BC的距离是（　　）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知二面角为，，，A为垂足，，，，则异面直线与所成角的余弦值为

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图，已知六棱锥P－ABCDEF的底面是正六边形，PA⊥平面ABC，PA＝2AB，则下列结论正确的是(　　)

    A．PB⊥AD
    B．平面PAB⊥平面PBC
    C．直线BC∥平面PAE
    D．直线PD与平面ABC所成的角为45°

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2))，则在空间四面体ABCD中，AD与BC的位置关系是(　　)

    A．相交且垂直B．相交但不垂直
    C．异面且垂直D．异面但不垂直

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    [2012·陕西高考]如图所示，在空间直角坐标系中有直三棱柱ABC－A1B1C1，CA＝CC1＝2CB，则直线BC1与直线AB1夹角的余弦值为(　　)

    A． B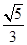． C． D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    [2013·广东高考]设m，n是两条不同的直线，α，β是两个不同的平面．下列命题中正确的是(　　)

    A．若α⊥β，m?α，n?β，则m⊥n 
    B．若α∥β，m?α，n?β，则m∥n 
    C．若m⊥n，m?α，n?β，则α⊥β 
    D．若m⊥α，m∥n，n∥β，则α⊥β 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    （2013•浙江）设m、n是两条不同的直线，α、β是两个不同的平面，（　　）

    A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥β C．若m∥n，m⊥α，则n⊥α D．若m∥α，α⊥β，则m⊥β

    查看答案和解析>>

    同步练习册答案