
 x2(1-x).
x2(1-x). ;
; f(x-1),x∈[n,n+1],则(x-n)∈[0,1]
f(x-1),x∈[n,n+1],则(x-n)∈[0,1] (x-n)2(1+n-x).
(x-n)2(1+n-x). f(x-1)=
f(x-1)= f(x-2)=…=
f(x-2)=…= f(x-n)=
f(x-n)=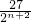 (x-n)2(1+n-x).(n=0也适用).…(4分)
(x-n)2(1+n-x).(n=0也适用).…(4分)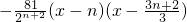 ,由f'(x)=0得x=n或x=n+
,由f'(x)=0得x=n或x=n+
| x | n | (n,n+ ) ) | n+ | (n+ ,n+1) ,n+1) | n+1 |
| f'(x) | + | 0 | - | + | |
| 0 | ↗ | 极大 | ↘ | 0 |
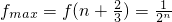 ,
, (x∈[n,n+1]).…(8分)
(x∈[n,n+1]).…(8分)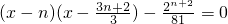 在[n,n+1]内是否有解.…(11分)
在[n,n+1]内是否有解.…(11分)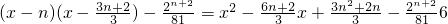 ,
, ∈[n,n+1],
∈[n,n+1],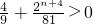 ,g(n)=
,g(n)=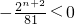 ,g(n+1)=
,g(n+1)=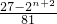 ,
, (x-n)2(1+n-x).通过递推关系式求出f(x)的解析式;
(x-n)2(1+n-x).通过递推关系式求出f(x)的解析式; ,即可证明对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤
,即可证明对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 27 |
| 4 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省郴州市汝城一中高三(上)周练数学试卷(4)(理科)(解析版) 题型:解答题
 ,且当x∈[0,1]时,f(x)=27x2(1-x).
,且当x∈[0,1]时,f(x)=27x2(1-x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com