
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点.
(1)若以![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,求椭圆的长轴长;
,求椭圆的长轴长;
(2)当![]() 时,问在
时,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?并说明理由.
为定值?并说明理由.
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且点
,且点![]() 到椭圆
到椭圆![]() 上任意一点的最大距离为3,椭圆
上任意一点的最大距离为3,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与以线段
与以线段![]() 为直径的圆相交于
为直径的圆相交于![]() 、
、![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 、
、![]() ,且
,且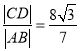 ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为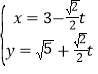 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这50件产品尺寸的样本平均数![]() .(同一组中的数据用该组区间的中点值作代表);
.(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() .
.
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则
![]() ,
,![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: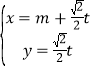 (
(![]() 是参数,
是参数,![]() 是常数).以
是常数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
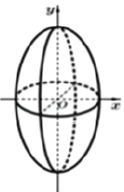
【题目】祖暅是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容易.”这里的“幂”指水平截面的面积.“势”指高,这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。于是可把半径相等的半球(底面在下)和圆柱(圆柱高等于半径)放在同一水平面上,圆柱里再放一个半径和高都与圆柱相等的圆锥(锥尖朝下),考察圆柱里被圆锥截剩的立体,这样在同一高度用平行平面截得的半球截面和圆柱中剩余立体截得的截面面积相等,因此半球的体积等于圆柱中剩余立体的体积.设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com