
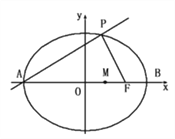
【题目】如图,A、B分别是椭圆![]() 的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
【答案】(1)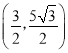 (2)
(2)![]()
【解析】试题分析:(1)先求出PA、F的坐标,设出P的坐标,求出![]() 、
、![]() 的坐标,由题意可得
的坐标,由题意可得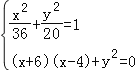 ,且y>0,
,且y>0,
解方程组求得点P的坐标.
(2)求出直线AP的方程,设点M的坐标,由M到直线AP的距离等于|MB|,求出点M的坐标,再求出椭圆上的点到点M的距离d的平方得解析式,配方求得最小值.
试题解析:
(1)由已知可得点A(﹣6,0),F(4,0),设点P(x,y),则![]() =(x+6,y),
=(x+6,y),![]() =(x﹣4,y).
=(x﹣4,y).
由已知可得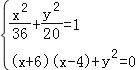 ,2x2+9x﹣18=0,解得x=
,2x2+9x﹣18=0,解得x=![]() ,或x=﹣6.
,或x=﹣6.
由于y>0,只能x=![]() ,于是y=
,于是y=![]() .∴点P的坐标是
.∴点P的坐标是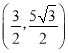 .
.
(2)直线AP的方程是  ,即 x﹣
,即 x﹣![]() y+6=0.
y+6=0.
设点M(m,0),则M到直线AP的距离是![]() .
.
于是![]() =|6﹣m|,又﹣6≤m≤6,解得m=2,故点M(2,0).
=|6﹣m|,又﹣6≤m≤6,解得m=2,故点M(2,0).
设椭圆上的点(x,y)到点M的距离为d,有 d2=(x﹣2)2+y2 =x2﹣4x+4+20﹣![]() x2 =
x2 =![]() (x﹣
(x﹣![]() )2+15,
)2+15,
∴当x=![]() 时,d取得最小值
时,d取得最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取![]() 份;
份;
②已知命题![]() ,则
,则![]() :
:![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件.
”的充要条件.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约( ) 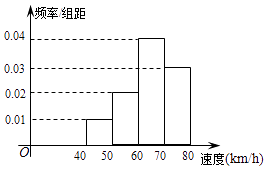
A.60辆
B.80辆
C.100辆
D.120辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 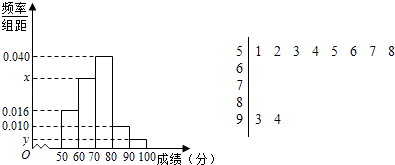
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切.
相切.
⑴求椭圆C的标准方程;
⑵已知点A、B为动直线![]() 与椭圆C的两个交点,问:在x轴上是否存在定点E,使得
与椭圆C的两个交点,问:在x轴上是否存在定点E,使得![]() 为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() 满足
满足![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 中心
中心![]() 点,将
点,将![]() 沿边
沿边![]() 折起,使
折起,使![]() 点至
点至![]() 点,已知
点,已知![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
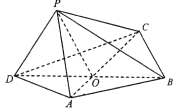
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求已知二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com