
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区共100名观众,得到如下的
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区共100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
A | 30 | y | |
B | x | z | |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35,且
地区当中“非常满意”的观众的概率为0.35,且![]() .请完成上述表格,并根据表格判断是否有95%的把握认为观众的满意程度与所在地区有关系?
.请完成上述表格,并根据表格判断是否有95%的把握认为观众的满意程度与所在地区有关系?
附:参考公式:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】[2018·临川一中]海盗船是一种绕水平轴往复摆动的游乐项目,因其外形仿照古代海盗船而得名.现有甲、乙两游乐场统计了一天6个时间点参与海盗船游玩的游客数量,具体数据如表:
时间点 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
甲游乐场 | 10 | 3 | 12 | 6 | 12 | 20 |
乙游乐场 | 13 | 4 | 3 | 2 | 6 | 19 |
(1)从所给6个时间点中任选一个,求参与海盗船游玩的游客数量甲游乐场比乙游乐场少的概率;
(2)记甲、乙两游乐场6个时间点参与海盗船游玩的游客数量分别为![]() ,
,![]() (
(![]() ),现从该6个时间点中任取2个,求恰有1个时间点满足
),现从该6个时间点中任取2个,求恰有1个时间点满足![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面ABCD是边长为a的菱形,
的底面ABCD是边长为a的菱形,![]() 面ABCD,
面ABCD,![]() ,E,F分别是CD,PC的中点.
,E,F分别是CD,PC的中点.

(1)求证:平面![]() 平面PAB;
平面PAB;
(2)M是PB上的动点,EM与平面PAB所成的最大角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为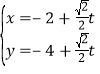 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记直线
,记直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)证明:![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)若棱![]() 上存在一点
上存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
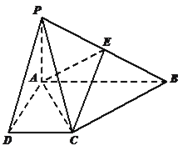
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店对过去100天其实体店和网店的销售量(单位:件)进行了统计,制成频率分布直方图如下:
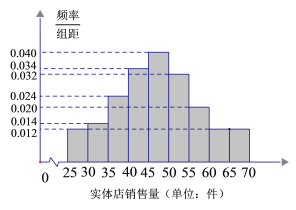
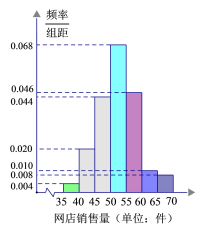
(1)若将上述频率视为概率,已知该服装店过去100天的销售中,实体店和网店销售量都不低于50件的概率为0.24,求过去100天的销售中,实体店和网店至少有一边销售量不低于50件的天数;
(2)若将上述频率视为概率,已知该服装店实体店每天的人工成本为500元,门市成本为1200元,每售出一件利润为50元,求该门市一天获利不低于800元的概率;
(3)根据销售量的频率分布直方图,求该服装店网店销售量中位数的估计值(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 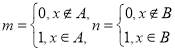 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,把圆
,把圆![]() 上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,且倾斜角为
,且倾斜角为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)当![]() 时,求曲线
时,求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的参数方程;
的参数方程;
(2)求点![]() 到
到![]() 两点的距离之积的最小值.
两点的距离之积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com