
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: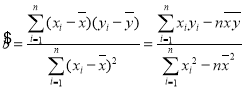 ,
,![]() )
)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为
是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上马云2016年10月份的收入
,如果再加上马云2016年10月份的收入![]() (约100亿元),则相对于
(约100亿元),则相对于![]() 、
、![]() 、
、![]() ,这101个月收入数据( )
,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
查看答案和解析>>
科目:高中数学 来源: 题型:
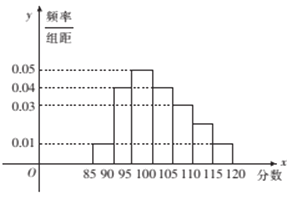
【题目】某校高二奥赛班![]() 名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
(1)求总人数![]() 和分数在110-115分的人数
和分数在110-115分的人数![]() ;
;
(2)现准备从分数在110-115的![]() 名学生(女生占
名学生(女生占![]() )中任选3人,求其中恰好含有一名女生的概率;
)中任选3人,求其中恰好含有一名女生的概率;
(3)为了分析某个学生的学习状态,对其下一阶段的学生提供指导性建议,对他前7次考试的数学成绩![]() (满分150分),物理成绩
(满分150分),物理成绩![]() 进行分析,下面是该生7次考试的成绩.
进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() ,
,![]() ……
……![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: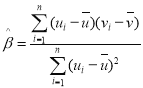 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为![]() 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰![]() ,其中
,其中![]() 为圆心,
为圆心, ![]() 在圆的直径上,
在圆的直径上, ![]() 在半圆周上,如图.
在半圆周上,如图.
(1)设![]() ,征地面积为
,征地面积为![]() ,求
,求![]() 的表达式,并写出定义域;
的表达式,并写出定义域;
(2)当![]() 满足
满足![]() 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,点D是AB的中点
=4,点D是AB的中点

(1)求证:AC![]() BC
BC![]() ;
;
(2)求证:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com