
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 13 |
| 6 |
| 13 |
| 6 |
| 1 |
| 3 |
| 13 |
| 6 |
| 1 |
| 6 |
| 13 |
| 6 |
| 1 |
| 2 |
| 29 |
| 36 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010年江西省吉安市高二下学期期末考试(文科)数学卷 题型:解答题
(满分12分)
某大学毕业生参加某单位的应聘考试,考核依次分为笔试,面试、实际操作共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则被淘汰,三轮考核都通过才能被正式录用,设该大学毕业生通过一、二、三轮考核的概率分别为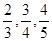 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
①求该大学毕业生进入第三轮考核的概率;
②设该大学毕业生在应聘考核中考核轮数为X,求X的概率分布列及期望和方差。
查看答案和解析>>
科目:高中数学 来源:2010年江西省吉安市高二下学期期末考试(文科)数学卷 题型:解答题
(满分12分)
某大学毕业生参加某单位的应聘考试,考核依次分为笔试,面试、实际操作共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则被淘汰,三轮考核都通过才能被正式录用,设该大学毕业生通过一、二、三轮考核的概率分别为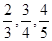 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
①求该大学毕业生进入第三轮考核的概率;
②设该大学毕业生在应聘考核中考核轮数为X,求X的概率分布列及期望和方差。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
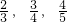 ,且各轮考核通过与否相互独立.
,且各轮考核通过与否相互独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com