
【题目】![]() 的内角
的内角 ![]() 的对边分别为
的对边分别为 ![]() ,已知
,已知 ![]() .
.![]()
(1)求 ∠![]() ;
;
(2)若 ![]() ,求
,求 ![]() 的面积
的面积 ![]() 的最大值.
的最大值.
【答案】
(1)
解:由已知及正弦定理可得 ![]() ,在
,在 ![]() 中,
中, ![]() , ∴
, ∴ ![]() ,
,
∴ ![]() ,
,
从而 ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ;
;
(2)
解法一:由(1)知 ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() (当且仅当
(当且仅当 ![]() 时等号成立),
时等号成立),
∴ ![]() ;
;
解法二:由正弦定理可知 ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() ,即
,即 ![]() 时,
时, ![]() 取最大值
取最大值 ![]() .
.
【解析】(1)利用正弦定理对已知的等式变形得: ![]() ,得到
,得到
sin(C- ![]() )=1,根据∠C的取值范围求出∠C的值。(2)利用正弦定理S=
)=1,根据∠C的取值范围求出∠C的值。(2)利用正弦定理S= ![]() absinC=
absinC= ![]() sinAsinB,然后根据角的范围来求S的最大值。
sinAsinB,然后根据角的范围来求S的最大值。
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是 ![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是 ![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中 ![]() 中,已知曲线
中,已知曲线 ![]() 经过点
经过点 ![]() ,其参数方程为
,其参数方程为 ![]() (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线 ![]() 的极坐标方程;
的极坐标方程;
(2)若直线 ![]() 交
交 ![]() 于点
于点 ![]() ,且
,且 ![]() ,求证:
,求证: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,且满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 , 数列{ ![]() }的前n项和Tn , 若Tn<M对一切正整数n都成立,则M的最小值为 .
}的前n项和Tn , 若Tn<M对一切正整数n都成立,则M的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点M(2,1),且离心率为
=1(a>b>0)过点M(2,1),且离心率为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)设A(0,﹣1),直线l与椭圆C交于P,Q两点,且|AP|=|AQ|,当△OPQ(O为坐标原点)的面积S最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形.将正方形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2. 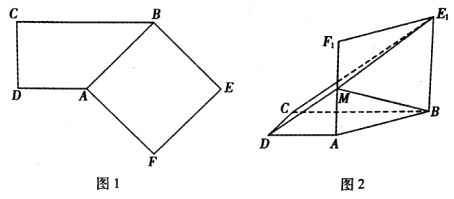
(I)求证:AC⊥BM;
(Ⅱ)求平面CE1M与平面ABE1F1所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com