
【题目】如图,在四棱锥![]() 中,
中,![]()
![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
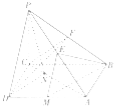
(1)求证:![]() ;
;
(2)已知点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一动点,当
上一动点,当![]() 为何值时,平面
为何值时,平面![]() ?
?
【答案】(1)证明见解析;(2)当![]() 时,平面
时,平面![]() .
.
【解析】
试题分析:(1)根据线面垂直的判定定理,若证![]() 平面
平面![]() ,则须证
,则须证![]() 垂直于平面
垂直于平面![]() 内的两条相交直线.根据题意,易证
内的两条相交直线.根据题意,易证![]() ,
,![]() ,又
,又![]() ,从而问题可得证;(2)根据题意,过点
,从而问题可得证;(2)根据题意,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,因为
,因为![]() 是
是![]() 的中点,所以易证平面
的中点,所以易证平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,又在矩形
,又在矩形![]() 中,易求得
中,易求得![]() ,当
,当![]() 是
是![]() 与
与![]() 的交点时,即
的交点时,即![]() 时,平面
时,平面![]() .
.
试题解析:(1)证明:∵![]() ,底面
,底面![]() 是矩形,
是矩形,
∴![]() ,又
,又![]() ,∴
,∴![]() ,………………2分
,………………2分
∴![]() .………………………………………………4分
.………………………………………………4分
∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() .………………………………5分
.………………………………5分
∵![]() ,∴
,∴![]() .……………………………………6分
.……………………………………6分
(2)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,………………………………7分
,………………………………7分
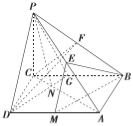
∵∴![]() ,……………………………………8分
,……………………………………8分
∵![]() ,∴
,∴![]() ,……………………………………9分
,……………………………………9分
∴当![]() 是
是![]() 与
与![]() 的交点时,平面
的交点时,平面![]() ,…………………………………………10分
,…………………………………………10分
在矩形![]() 中,求得
中,求得![]() .……………………………………12分
.……………………………………12分


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y﹣1=0,l2:2x+ny+5=0,l3:mx+3y+1=0,若l1∥l2且l1⊥l3,则m+n的值为( )
A.﹣10B.﹣2C.2D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() 三个数中任取的一个数,求
三个数中任取的一个数,求![]() 不为空集的概率;
不为空集的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 不为空集的概率.
不为空集的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在D上的函数f(x)满足:对任意x∈D,存在常数M>0,都有-M<f(x)<M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界。
(Ⅰ)判断函数f(x)=![]() -2x+2,x∈[0,2]是否是有界函数,请说明理由;
-2x+2,x∈[0,2]是否是有界函数,请说明理由;
(Ⅱ)若函数f(x)=1+![]() +
+![]() ,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
,x∈[0,+∞)是以3为上界的有界函数,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生的视力情况,现采用随机抽样的方式从该校的![]() 两班中各抽5名学生进行视力检测,检测的数据如下:
两班中各抽5名学生进行视力检测,检测的数据如下:
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是:![]() .
.
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是:![]() .
.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?并计算![]() 班的5名学生视力的方差;
班的5名学生视力的方差;
(2)现从![]() 班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于
班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和面内一点
,和面内一点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,试求
,试求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lg(ax2+2x+1) .
(1)若函数f (x)的定义域为R,求实数a的取值范围;
(2)若函数f (x)的值域为R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com