
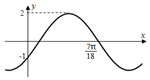
 函数f(x)=Asin(ωx+ϕ)($A>0,ω>0,|ϕ|<\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+ϕ)($A>0,ω>0,|ϕ|<\frac{π}{2}$)的部分图象如图所示.分析 (1)由函数图象得A=2,$sinϕ=-\frac{1}{2}$,结合范围$|ϕ|<\frac{π}{2}$,可求ϕ,由$f(\frac{7π}{18})=0$,结合$\frac{1}{2}•\frac{2π}{ω}<\frac{7π}{18}<\frac{2π}{ω}$,可求ω,即可得解函数解析式.
(2)由题意利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)由函数图象可得:A=2,f(0)=-1,
∴$sinϕ=-\frac{1}{2}$,
∵$|ϕ|<\frac{π}{2}$,
∴$ϕ=-\frac{π}{6}$,
∵$f(\frac{7π}{18})=0$,
∴$\frac{7π}{18}•ω-\frac{π}{6}=kπ(k∈Z)$,…(3分)
∴$ω=\frac{18}{7}k+\frac{3}{7}$,
∵$\frac{1}{2}•\frac{2π}{ω}<\frac{7π}{18}<\frac{2π}{ω}$,
∴k=1,ω=3,…(5分)
∴$f(x)=2sin(3x-\frac{π}{6})$.…(6分)
(2)把y=sinx(x∈R)的图象向右平移$\frac{π}{6}$个单位,可得y=sin(x-$\frac{π}{6}$)的图象;
把所得图象上各点的横坐标变为原来的$\frac{1}{3}$倍,可得y=sin(3x+$\frac{π}{6}$)的图象;
再把所得图象上各点的纵坐标变为原来的2倍,可得y=2sin(3x+$\frac{π}{6}$)的图象.
(三步每步表述及解析式正确各2分,前面的步骤错误,后面的正确步骤分值减半).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换规律的应用,属于基础题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ±3 | B. | ±$\frac{9}{2}$ | C. | 3 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}$倍 | B. | 10倍 | C. | ${10^{\frac{7}{6}}}$倍 | D. | $ln\frac{7}{6}$倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com