
分析 分别取x=1,2,3,得出相应的价格表达式,归纳出,经过x个月后,价格为:a(1-p%)x,x≤m.
解答 解:根据题意,因为原价为a元,价格每月减少p%,因此,
经过以一个月后(x=1),价格为:a(1-p%),
再过一个月后(x=2),价格为:a(1-p%)(1-p%),
再过一个月后(x=3),价格为:a(1-p%)(1-p%)(1-p%),
…
经过x个月后,价格为:a(1-p%)x,x≤m,
所以,价格y元随月数x变化的函数解析式为:y=a(1-p%)x(0≤x≤m).
故答案为:y=a(1-p%)x(0≤x≤m).
点评 本题主要考查了函数解析式的求解及常用方法,通过自变量x=1,2,3,观察出表达式的特征,归纳出函数的解析式,属于基础题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
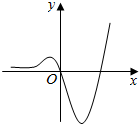
| A. | y=2x-x2-1 | B. | y=$\frac{x}{lnx}$ | C. | y=$\frac{{2}^{x}sinx}{{4}^{x}+1}$ | D. | y=(x2-2x)ex |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com