
 以O为原点,
以O为原点,| OA |
| OA |
| AG |
| OG |
| OA |
| AG |
| AG |
| OA |
| OA |
| AG |
| 1 |
| t |
| OG |
| y2 |
| b2 |
| 9 |
| b2 |
| OG |
| y2 |
| 3 |
|
| 2k |
| 3-k2 |
| -4 |
| 3-k2 |
| -4(1+k2) |
| 3-k2 |
| 2k2 |
| 3-k2 |
| 1 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
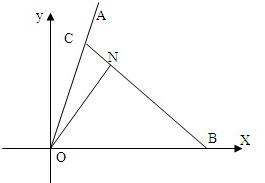 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中sina=
如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中sina=
| ||
| 10 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| AB |
| AB |
| AB |
| x2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中
如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中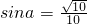 ,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中
,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中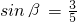 ,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.
,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.查看答案和解析>>
科目:高中数学 来源:2009-2010学年高三强化班数学寒假作业(直线及其方程)(解析版) 题型:解答题
 ,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中
,在距离O地5a(a为正常数)千米,北偏东β角的N处住有一位医学专家,其中 ,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.
,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇.经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com