练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆，以椭圆的顶点为顶点的四边形的面积为，且该四边形内切圆的半径为.

    （1）求椭圆的方程；

    （2）设是过椭圆中心的任意一条弦，直线是线段的垂直平分线，若是直线与椭圆的一个交点，求面积的最小值.

    【答案】（1）；（2）.

    【解析】

    （1）由已知条件列出的方程组，解得后得椭圆方程；

    （2）当不在坐标轴上时，设直线的方程为：，设，

    代入椭圆方程求出交点坐标，得弦长，同理得点坐标得，然后计算三角形面积，利用基本不等式得最小值．再求出直线与坐标轴重合时，三角形的面积，比较后可得最小值．

    （1）

    ∴椭圆的标准方程为

    （2）当不在坐标轴上时，设直线的方程为：，设，

    ，

    同理：，

    ∴

    ∵

    （当且仅当，即进“=”成立）

    ∴，

    当直线与坐标轴生重合时，易得，

    ∵

    ∴当且仅当时，面积的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着年北京冬奥会临近，中国冰雪产业快速发展，冰雪运动人数快速上升，冰雪运动市场需求得到释放，将引领户外用品行业市场增长．下面是年至年中国雪场滑雪人次（万人次）与同比增长率的统计图，则下面结论中不正确的是（ ）

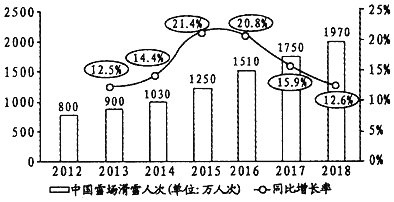
    A.年至年，中国雪场滑雪人次逐年增加

    B.年至年，中国雪场滑雪人次和同比增长率均逐年增加

    C.年与年相比，中国雪场滑雪人次的同比增长率近似相等，所以同比增长人数也近似相等

    D.年与年相比，中国雪场滑雪人次增长率约为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图①，在平面五边形中，是梯形，，，，，是等边三角形.现将沿折起，连接、得如图②的几何体.

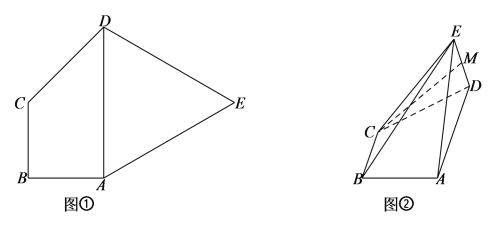
    （1）若点是的中点，求证：平面；

    （2）若，在棱上是否存在点，使得二面角的余弦值为？若存在，求的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面为直角梯形，，，，，平面平面，点在上，且．


    （Ⅰ）证明：平面平面；

    （Ⅱ）当异面直线与所成角的余弦值为时，求二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）当时，求的单调区间；

    （Ⅱ）若的值域为，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分14分）已知过原点的动直线与圆 相交于不同的两点，．

    （1）求圆的圆心坐标；

    （2）求线段的中点的轨迹的方程；

    （3）是否存在实数，使得直线 与曲线只有一个交点？若存在，求出的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是

    A. y与x具有正的线性相关关系

    B. 回归直线过样本点的中心（，）

    C. 若该大学某女生身高增加1cm，则其体重约增加0.85kg

    D. 若该大学某女生身高为170cm，则可断定其体重比为58.79kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数在处取得极大值或极小值，则称为函数的极值点.已知函数.

    （1）当时，求的极值；

    （2）若在区间上有且只有一个极值点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个正四面体和一个正四棱锥，它们的各条棱长均相等，则下列说法：

    ①它们的高相等；②它们的内切球半径相等；③它们的侧棱与底面所成的线面角的大小相等；④若正四面体的体积为，正四棱锥的体积为，则；⑤它们能拼成一个斜三棱柱.其中正确的个数为（ ）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    同步练习册答案