
【题目】已知两点A(﹣2,0)、B(2,0),动点P满足![]() .
.
(1)求动点P的轨迹Ω的方程;
(2)若椭圆![]() 上点(x0,y0)处的切线方程是
上点(x0,y0)处的切线方程是![]() :
:
①过直线l:x=4上一点M引Ω的两条切线,切点分别是P、Q,求证:直线PQ恒过定点N;
②是否存在实数λ,使得|PN|+|QN|=λ|PN||QN|?若存在,求出λ的值;若不存在,说明理由.
【答案】(1)![]() (y≠0);(2)①见解析②存在,
(y≠0);(2)①见解析②存在,![]()
【解析】
(1)设![]() ,再根据斜率之积列式求解即可.
,再根据斜率之积列式求解即可.
(2)①根据题中所给的切线方程,设![]() ,进而求得过
,进而求得过![]() 的切线方程,再代入
的切线方程,再代入![]() 坐标即可求得
坐标即可求得![]() 的直线方程,再分析定点即可.
的直线方程,再分析定点即可.
②由①有![]() ,代入椭圆方程求得交点
,代入椭圆方程求得交点![]() 关于纵坐标的韦达定理,进而表达出
关于纵坐标的韦达定理,进而表达出![]() 的关系式,再化简求解即可.
的关系式,再化简求解即可.
(1)设P(x,y),由题意kPAkPB![]() ,整理得:
,整理得:![]() (y≠0),
(y≠0),
所以动点P的轨迹Ω的方程:![]() (y≠0);
(y≠0);
(2)①设切点P(x1,y1),Q(x2,y2),由题意设M(4,t),则切线方程分别是:![]() ,
,![]() 1,
1,
因为两条切线过M点,则x1![]() 1,x2
1,x2![]() 1,
1,
即P,Q的坐标满足方程:x![]() y=1,而两点确定唯一的直线,
y=1,而两点确定唯一的直线,
所以直线PQ的方程:x![]() y=1,
y=1,
显然对任意的t值,点(1,0)都适合,
所以直线PQ恒过定点N(1,0);
②将直线PQ方程:x![]() y+1代入椭圆中整理得:3(
y+1代入椭圆中整理得:3(![]() 1)2+4y2﹣12=0,
1)2+4y2﹣12=0,
即(12+t2)y2﹣6ty﹣27=0
∴y1+y2![]() ,y1y2
,y1y2![]() ,设y1>0,y2<0,
,设y1>0,y2<0,
因为|PN|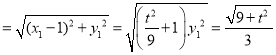 y1,
y1,
同理|QN|![]() ,
,
所以![]()
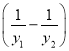
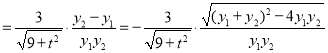
![]()
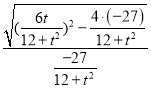
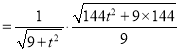
![]() .
.
即|PN|+|QN|![]() |PN||QN|
|PN||QN|
故存在实数![]() ,使得|PN|+|QN|=λ|PN||QN|恒成立.
,使得|PN|+|QN|=λ|PN||QN|恒成立.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】设X~N(μ1,![]() ),Y~N(μ2,
),Y~N(μ2,![]() ),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )
),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )

A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≥t)≥P(Y≥t)
D. 对任意正数t,P(X≤t)≥P(Y≤t)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: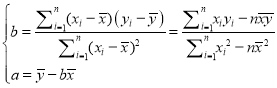
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若函数f(x)在![]() 处有极值,求函数f(x)的最大值;
处有极值,求函数f(x)的最大值;
(2)是否存在实数b,使得关于x的不等式![]() 在
在![]() 上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为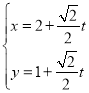 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() ,
,![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
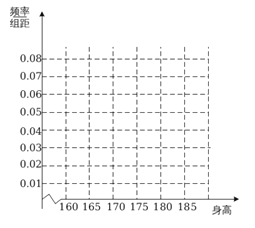
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋科学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有菱草垛、方垛、三角垛等等,某仓库中部分货物堆放成“菱草垛”,自上而下,第一层1件,以后每一层比上一层多1件,最后一层是![]() 件,已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的
件,已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的![]() ,若这堆货物总价是
,若这堆货物总价是![]() 万元,则
万元,则![]() 的值为________
的值为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com