
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�����ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������ľ�������ˮ����������λ���֣�����ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ���˽�ȫ����������ˮ���ֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���
�IJ��ְ�����շѣ�Ϊ���˽�ȫ����������ˮ���ֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���![]() ����
����![]() �ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ
�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ
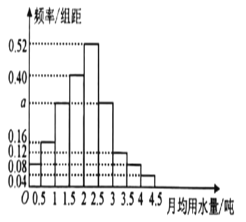
��1����Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2����������������ʹ85%�ľ���ÿ�µ���ˮ����������![]() ���֣�������
���֣�������![]() ��ֵ����˵�����ɡ�
��ֵ����˵�����ɡ�
���𰸡���1��0.30����2����������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������
��������
��1������Ƶ�ʷ�ֱ��ͼ�еľ�������ĺ�Ϊ1��![]() ����
����
��2���ȴ������һ��![]() ���ڵ����䣬�ٸ�������
���ڵ����䣬�ٸ�������![]() ��Ƶ��֮��Ϊ0.85�����
��Ƶ��֮��Ϊ0.85�����![]() ��ֵ
��ֵ
��1����ֱ��ͼ���ɵ�![]() ��
��
���![]() .
.
��2����Ϊǰ6��Ƶ��֮��Ϊ
![]()
��ǰ5���Ƶ��֮��Ϊ
![]()
����![]() .
.
��![]()
���![]() .��ˣ���������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������.
.��ˣ���������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������.


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����z����|z|![]() ��z��ʵ������0��z2���鲿Ϊ2.
��z��ʵ������0��z2���鲿Ϊ2.
��1������z��
��2���踴��z��z2��z��z2֮�ڸ�ƽ���϶�Ӧ�ĵ�ֱ�ΪA��B��C����![]() ��
��![]()
![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ����ĩ��ѧ�����У�Ϊͳ��ѧ���Ŀ����������ѧУ��2000��ѧ���������ȡ50��ѧ���Ŀ��Գɼ�������ѧ���ɼ�ȫ������65�ֵ�145��֮�䣨����150�֣�����ͳ�ƽ�������·�ʽ�ֳɰ��飺��һ��![]() ��
��![]() ���ڶ���
���ڶ���![]() ��
��![]() ��
��![]() �ڰ���
�ڰ���![]() ��
��![]() ����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�
����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣�
��1����������Ƶ�ʣ������Ƶ�ʷֲ�ֱ��ͼ��
��2�����������ݹ��Ƹ�У��2000��ѧ����ο��Գɼ���ƽ���֣�ͬһ���е������ø���������е�ֵ������������ƽ��ֵ����
��3�����������ɼ����ڵ�����͵ڰ��������ѧ���������ȡ2���������ǵķֲ�ľ���ֵС��10�ֵĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ijԲ�ļ����귽��Ϊ![]() ����
����
(1)Բ����ͨ���̺Ͳ���������
(2)Բ�����е�![]() ��
��![]() �����ֵ����Сֵ.
�����ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxoy�У���֪����C��![]() ��
��![]() Ϊ��������������ԭ��Ϊ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
Ϊ��������������ԭ��Ϊ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
��1��������C�ļ����귽�̣���A��BΪ����C�ϵ����㣬֤����![]() ʱ��
ʱ��![]() ��ֵ��
��ֵ��
��2��������![]() ����б��Ϊ
����б��Ϊ![]() ��ֱ��l������C�ཻ��A��B���㣬��
��ֱ��l������C�ཻ��A��B���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��ƽ��
��ƽ��![]() ����
����![]() ��
��![]() .
.![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬��֤��
���е㣬��֤��

����![]() ����
����![]() ��
��
����![]() ƽ��
ƽ��![]() ��
��
����ƽ��![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡijУҪ����һ���¿���һ�㿼�����뿼5��ѧ�ƣ����������Ӣ���ۺ����Ŀ��DZؿ���Ŀ������һ������������ѧ�����Ρ���ʷ�����������Ӣ��2��ѡ��.Ϊ��ʡʱ�䣬����ÿ�����翼���ţ����翼һ��ѧ�ƣ�����뿼��.
��1���������Ӣ���ۺ�����ѧ�ư����������һ�����ԣ����������ճ̰��ű����ж����ֲ�ͬ�İ��ŷ�����
��2��������ƿ���˳�������ƣ�����ѧ����ѧ��ͬһ�쿼�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ƕ�����R�ϵ�ż�������ҵ�
�Ƕ�����R�ϵ�ż�������ҵ�![]() ʱ��
ʱ��![]() ��
��![]() ��.
��.
��1����![]() ʱ����
ʱ����![]() �ı���ʽ��
�ı���ʽ��
��2����![]() ������
������![]() �����ֵ
�����ֵ![]() �ı���ʽ��
�ı���ʽ��
��3����![]() ʱ��������x�ķ���
ʱ��������x�ķ���![]() ��a��
��a��![]() ��ǡ��10����ͬʵ���⣬��a��ȡֵ��Χ.
��ǡ��10����ͬʵ���⣬��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������15��ʡ����ѧ������ָ�1��2��3��4���ĸ��༶������1������2�����2�ࡢ4��ÿ������3�����3�����2���������_________�ֲ�ͬ���䷽��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com