
【题目】将函数y=sin(x+ ![]() )的图象上各点的横坐标压缩为原来的
)的图象上各点的横坐标压缩为原来的 ![]() 倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
【答案】A
【解析】解:将函数y=sin(x+ ![]() )图象上每一点的横坐标缩短到原来的
)图象上每一点的横坐标缩短到原来的 ![]() (纵坐标不变),得到函数y=sin(2x+
(纵坐标不变),得到函数y=sin(2x+ ![]() )的图象;
)的图象;
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数g(x)的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈z,
],k∈z,
当k=0时,可得函数在区间(﹣ ![]() ,
, ![]() )单调递增.
)单调递增.
故选:A.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是椭圆C: ![]() (a>b>0)的两个焦点,P(1,
(a>b>0)的两个焦点,P(1, ![]() )是椭圆上一点,且
)是椭圆上一点,且 ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差数列.
|PF2|成等差数列.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F2 , 且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得 ![]()
![]() =﹣
=﹣ ![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2 ![]() sinθ.
sinθ.
(1)求圆C的直角做标方程;
(2)圆C的圆心为C,点P为直线l上的动点,求|PC|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区准备将闲置的一直角三角形地块开发成公共绿地,图中![]() .设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道
.设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ).现考虑方便和绿地最大化原则,要求点
).现考虑方便和绿地最大化原则,要求点![]() 与点
与点![]() 均不重合,
均不重合,![]() 落在边
落在边![]() 上且不与端点
上且不与端点![]() 重合,设
重合,设![]() .
.
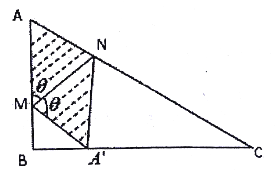
(1)若![]() ,求此时公共绿地的面积;
,求此时公共绿地的面积;
(2)为方便小区居民的行走,设计时要求![]() 的长度最短,求此时绿地公共走道
的长度最短,求此时绿地公共走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=x2-2mx+4在[2,+∞)上单调递增,命题q:关于x的不等式mx2+4(m-2)x+4>0的解集为R.若p∨q为真命题,p∧q为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且c= ![]() asinC﹣ccosA
asinC﹣ccosA
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= ![]() DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC= ![]() AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB. 
(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①函数y=![]() 的定义域为{x|x≥1};
的定义域为{x|x≥1};
②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xetx﹣ex+1,其中t∈R,e是自然对数的底数.
(1)若方程f(x)=1无实数根,求实数t的取值范围;
(2)若函数f(x)在(0,+∞)内为减函数,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com