设某银行一年内吸纳储户存款的总数与银行付给储户年利率的平方成正比,若该银行在吸纳到储户存款后即以5%的年利率把储户存款总数的90%贷出以获取利润,问银行支付给储户年利率定为多少时,才能获得最大利润?
(注:银行获得的年利润是贷出款额的年利息与支付给储户的年利息之差.)
解:设银行支付给储户的年利率为x,银行获得的年利润为y,
则y=kx2×0.9×0.05-kx2•x=0.045kx2-kx3(x>0).
y'=0.09kx-3kx2=3kx(0.03-x),
令y'=0,得x=0.03,
当x<0.03时,y'>0;
当x>0.03时,y'<0.
故当x=0.03时,y取极大值,
并且这个极大值就是函数y的最大值.
所以,当银行支付给储户年利率为3%时,银行可获得的年利润.
分析:设银行支付给储户的年利率为x,银行获得的年利润为y,则y=kx2×0.9×0.05-kx2•x=0.045kx2-kx3(x>0).y'=0.09kx-3kx2=3kx(0.03-x),令y'=0,得x=0.03,由此能求出当银行支付给储户年利率为3%时,银行可获得的年利润.
点评:本题考查函数的生产实际中的具体应用,是中档题.解题时要认真审题,注意寻找数理量间的等价关系,合理地建立方程.恰当地利用导数的性质进行求解.



 ________Z;
________Z;  ________Q;
________Q;  ________Q;
________Q;  ________R;
________R;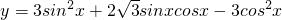 ,(x∈R),
,(x∈R),