
【题目】已知圆心在 ![]() 轴上的圆
轴上的圆 ![]() 过点
过点 ![]() 和
和 ![]() ,圆
,圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)由圆 ![]() 上的动点
上的动点 ![]() 向圆
向圆 ![]() 作两条切线分别交
作两条切线分别交 ![]() 轴于
轴于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)设 , ,
依题意得,圆 的圆心为线段 的垂直平分线 ![]() 与 轴的交点 .
与 轴的交点 .
因为直线 ![]() 的方程为 ,即 ,
的方程为 ,即 ,
所以圆心 的坐标为 .
所以圆 的方程为 .
(2)设圆 上的动点 的坐标为 ,
则 ,
即 ,
解得 .
设点 , ,
则直线 : ,即 ,
因为直线 与圆 相切,所以 ,
化简得 . ①
同理得 , ②
由①②知 , 为方程 的两根,
即 
所以
.
因为 ,
所以
.
令 ,因为 ,所以 .
所以 ,
当 时, ![]() ,
,
当 时, .
所以 的取值范围为 .
【解析】分析:本题主要考查了圆方程的综合应用,解决问题的关键是(1)先设圆的标准方程,再利用已知条件可得 ![]() 和
和 ![]() 的值,即可得圆
的值,即可得圆 ![]() 的方程;(2)先设圆
的方程;(2)先设圆 ![]() 上的动点
上的动点 ![]() 的坐标为
的坐标为 ![]() ,则可得
,则可得 ![]() 的取值范围,再写出
的取值范围,再写出 ![]() ,
, ![]() 的方程,可得
的方程,可得 ![]() 和
和 ![]() 的坐标,进而可得
的坐标,进而可得 ![]() ,利用函数的单调性,可得
,利用函数的单调性,可得 ![]() 的最大值和最小值,即可得
的最大值和最小值,即可得 ![]() 的取值范围.
的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.
(1)求红队至少两名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,能推断这个几何体可能是三棱台的是( ) 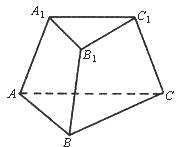
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1 , BC=B1C1 , CA=C1A1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣ ![]() .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为 . 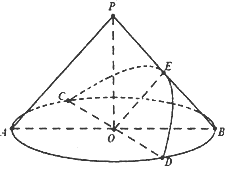
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com