练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)的导函数的图象如

    右图所示，则下列说法正确的是

    A．函数在内单调递增

    B．函数在内单调递减

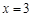    C．函数在处取极大值

    D．函数在处取极小值

     

    【答案】

    B

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：广东省深圳高级中学2011－2012学年高二上学期期中测试数学文科试题 题型：013

    函数f(x)的导函数的图象如图所示，则下列说法正确的是

    [　　]
    A．

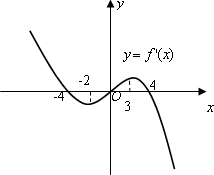
    函数f(x)在(－4，0)内单调递减

    B．

    函数f(x)在(－2，3)内单调递增

    C．

    函数f(x)在x＝3处取极大值

    D．

    函数f(x)在x＝4处取极小值

    查看答案和解析>>

    科目：高中数学 来源：甘肃省武威六中2012届高三第二次诊断性考试数学理科试题 题型：022

    函数f(x)的导函数为(x)，若对于定义域内任意x1，x2(x1≠x2)，有恒成立，则称f(x)为恒均变函数．给出下列函数：

    ①f(x)＝2x＋3；

    ②f(x)＝x2－2x＋3；

    ③；

    ④f(x)＝ex；

    ⑤f(x)＝lnx．其中为恒均变函数的序号是________．(写出所有满足条件的函数的序号)

    查看答案和解析>>

    科目：高中数学 来源：福建省泉州一中2012届高三5月模拟考试数学理科试题 题型：022

    函数f(x)的导函数为(x)，若对于定义域内任意x1、x2(x1≠x2)，有恒成立，则称f(x)为恒均变函数．给出下列函数：

    ①f(x)＝2x＋3；

    ②f(x)＝x2－2x＋3；

    ③f(x)＝；

    ④f(x)＝ex；

    ⑤f(x)＝lnx．

    其中为恒均变函数的序号是________．(写出所有满足条件的函数的序号)

    查看答案和解析>>

    科目：高中数学 来源：2013届江西省高二下学期第一次月考文科数学试卷 题型：选择题

    （普通班）函数f(x)的定义域为R，f(－1)＝2，对任意x∈R，f′(x)>2，则f(x)>2x＋4的解集为(　　)

    A．(－1,1)        B．(－1，＋∞)        C．(－∞，－1)         D．(－∞，＋∞)

    （实验班）已知可导函数的导函数为，且满足：①，②，记，，，则的大小顺序为（   ）

    A.    B.     C.    D.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=-x3+ax2-4(a∈R).

    (1)若函数y=f(x)的图象在点P(1,f(1))处的切线的倾斜角为,求a;

    (2)设f(x)的导函数是f′(x).在(1)的条件下,若m,n∈［-1,1］,求f(m)+f′(n)的最小值;

    (3)若存在x0∈(0,+∞),使f(x0)＞0,求a的取值范围.

    查看答案和解析>>

    同步练习册答案