【题目】已知F1 ， F2为椭圆 
的左、右焦点，F2在以 
为圆心，1为半径的圆C2上，且|QF1|+|QF2|=2a．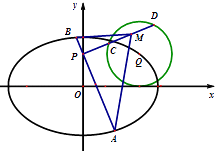
（1）求椭圆C1的方程；
（2）过点P（0，1）的直线l1交椭圆C1于A，B两点，过P与l1垂直的直线l2交圆C2于C，D两点，M为线段CD中点，求△MAB面积的取值范围．
【答案】
（1）
解：圆C2的方程为 
，
此圆与x轴相切，切点为 
∴ 
，即a2﹣b2=2，且 
， 
又|QF1|+|QF2|=3+1=2a．
∴a=2，b2=a2﹣c2=2
∴椭圆C1的方程为 
．
（2）
解：当l1平行x轴的时候，l2与圆C2无公共点，从而△MAB不存在；
设l1：x=t（y﹣1），则l2：tx+y﹣1=0．
由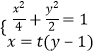 
，消去x得（t2+2）y2﹣2t2y+t2﹣4=0，
则 
．
又圆心 
到l2的距离 
，得t2＜1．
又MP⊥AB，QM⊥CD
∴M到AB的距离即Q到AB的距离，设为d2，
即 
．
∴△MAB面积 
令 
则 
．
∴△MAB面积的取值范围为 
．
【解析】（1）圆C2的方程为 ，由此圆与x轴相切，求出a，b的值，由此能求出椭圆C1的方程．（2）设l1：x=t（y﹣1），则l2：tx+y﹣1=0，与椭圆联立，得（t2+2）y2﹣2t2y+t2﹣4=0，由此利用弦长公式、点到直线距离公式，结合已知条件能求出△MAB面积的取值范围．
科目：高中数学 来源： 题型：
【题目】设函数f（x）=x2ex﹣1﹣ 
x3﹣x2（x∈R）．
（1）求函数f（x）的单调区间；
（2）当x∈（1，+∞）时，用数学归纳法证明：n∈N* ， ex﹣1＞ 
（其中n!=1×2×…×n）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的偶函数，且当x≥0时，f（x）=x|x﹣2|．若关于x的方程f2（x）+af（x）+b=0（a，b∈R）恰有10个不同实数解，则a的取值范围为（ ）
A.（0，2）
B.（﹣2，0）
C.（1，2）
D.（﹣2，﹣1）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知 
=（sinx，cosx）， 
=（sinx，k）， 
=（﹣2cosx，sinx﹣k）．
（1）当x∈[0， 
]时，求| + |的取值范围；
（2）若g（x）=（ + ） ，求当k为何值时，g（x）的最小值为﹣ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直三棱柱
中， 
， 
， 
是
的中点，△
是等腰三角形， 
为
的中点， 
为
上一点；
（1）若
∥平面
，求
；
（2）平面
将三棱柱
分成两个部分，求含有点
的那部分体积；
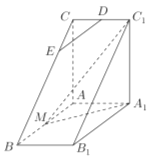
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数y=f（x）的定义域为{x|x∈R，且x≠2}，且y=f（x+2）是偶函数，当x＜2时，f（x）=|2x﹣1|，那么当x＞2时，函数f（x）的递减区间是（ ）
A.（3，5）
B.（3，+∞）
C.（2，+∞）
D.（2，4]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a，b，c分别为△ABC三个内角A，B，C所对的边长，且acosB+bcosA=2ccosC．
（1）求角C的值；
（2）若c=4，a+b=7，求S△ABC的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，椭圆
的离心率为
，其左顶点
在圆
上.
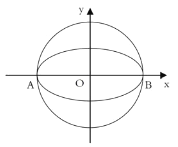
（1）求椭圆
的方程；
（2）直线
与椭圆的另一个交点为
，与圆
的另一个交点为
.
（ⅰ）当
时，求直线
的斜率；
（ⅱ）是否存在直线，使
？若存在，求出直线的斜率；若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
