
【题目】如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
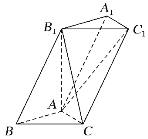
(I) 证明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1与平面BCB1所成角的正弦值.
【答案】(I)详见解析(II)![]()
【解析】
(Ⅰ)连结AB1,在△ABB1中,由余弦定理得求出AB1,通过计算勾股定理证明AB1⊥AB,以及证明AC⊥AB,推出AB⊥平面AB1C.得到AB⊥B1C.
(Ⅱ)以A为原点,以![]() 的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,求出平面BCB1的法向量,利用向量的数量积求解AC1与平面BCB1所成角的正弦值.
的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,求出平面BCB1的法向量,利用向量的数量积求解AC1与平面BCB1所成角的正弦值.
(I)证明:连接AB1,在△ABB1中,AB=1,BB1=2,∠ABB1=60°,

由余弦定理得,AB=AB2+BB-2AB·BB1·cos∠ABB1=3,
∴AB1=![]() ,∴BB=AB2+AB,
,∴BB=AB2+AB,
∴AB1⊥AB.
又△ABC为等腰直角三角形,且AB=AC,
∴AC⊥AB,∵AC∩AB1=A,
∴AB⊥平面AB1C.
(II)解:∵AB1=![]() ,AB=AC=1,B1C=2,
,AB=AC=1,B1C=2,
∴B1C2=AB+AC2,∴AB1⊥AC.
如图,以A为原点,以![]() ,
,![]() ,
,![]() 的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,则A(0,0,0),B1(0,0,
的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,则A(0,0,0),B1(0,0,![]() ),
),

B(1,0,0),C(0,1,0),
∴![]() =(-1,0,
=(-1,0,![]() ),
),
![]() =(-1,1,0).
=(-1,1,0).
设平面BCB1的一个法向量为n=(x,y,z),
由 得
得![]() 令z=1,得x=y=
令z=1,得x=y=![]() ,
,
∴平面BCB1的一个法向量为n=(![]() ,
,![]() ,1).
,1).
∵![]() =
=![]() +
+![]() =
=![]() +
+![]() =(0,1,0)+(-1,0,
=(0,1,0)+(-1,0,![]() )=(-1,1,
)=(-1,1,![]() ),
),
∴cos〈![]() ,n〉=
,n〉=![]() =
=![]() =
=![]() ,
,
∴AC1与平面BCB1所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.

(1)求频率分布直方图中a的值;
(2)估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图估计20名学生数学考试成绩的众数,平均数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,MN分别是边长为1的正方形ABCD的边BCCD的中点,将正方形沿对角线AC折起,使点D不在平面ABC内,则在翻折过程中,有以下结论:

①异面直线AC与BD所成的角为定值.
②存在某个位置,使得直线AD与直线BC垂直.
③存在某个位置,使得直线MN与平面ABC所成的角为45°.
④三棱锥M-ACN体积的最大值为![]() .
.
以上所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,抛物线C与直线l1:
的焦点为F,抛物线C与直线l1:![]() 的一个交点为
的一个交点为![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线C的方程;
(II)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A,B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月某城市国际马拉松赛正式举行,组委会对
月某城市国际马拉松赛正式举行,组委会对![]() 名裁判人员进(年龄均在
名裁判人员进(年龄均在![]() 岁到
岁到![]() 岁)行业务培训,现按年龄(单位:岁)进行分组统计:第
岁)行业务培训,现按年龄(单位:岁)进行分组统计:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如下:
,得到的频率分布直方图如下:
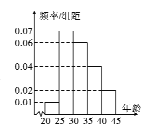
(1)若把这![]() 名裁判人员中年龄在
名裁判人员中年龄在![]() 称为青年组,其中男裁判
称为青年组,其中男裁判![]() 名;年龄在
名;年龄在![]() 的称为中年组,其中男裁判
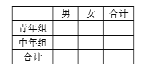
的称为中年组,其中男裁判![]() 名.试完成
名.试完成![]() 列联表并判断能否在犯错误的概率不超过
列联表并判断能否在犯错误的概率不超过![]() 的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
的前提下认为裁判员属于不同的组别(青年组或中年组)与性别有关系?
(2)培训前组委会用分层抽样调查方式在第![]() 组共抽取了
组共抽取了![]() 名裁判人员进行座谈,若将其中抽取的第
名裁判人员进行座谈,若将其中抽取的第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,若组委会决定从上述
,若组委会决定从上述![]() 名裁判人员中再随机选
名裁判人员中再随机选![]() 人参加新闻发布会,要求这
人参加新闻发布会,要求这![]() 组各选
组各选![]() 人,试求裁判人员
人,试求裁判人员![]() 不同时被选择的概率;
不同时被选择的概率;
附: 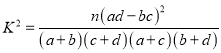
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为
的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为![]() ,|F1F2|=
,|F1F2|=![]() ,O为坐标原点.
,O为坐标原点.
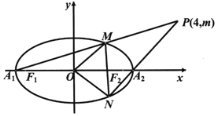
(1)求椭圆C的方程;
(2)设过点P(4,m)的直线PA1,PA2与椭圆分别交于点M,N,其中m>0,求![]() 的面积S的最大值.
的面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com