
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
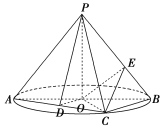
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明AC⊥DO,PO⊥AC,再证明AC⊥平面PDO;(2)当CO⊥AB时,C到AB的距离最大,且最大值为1,再求三棱锥P-ABC体积的最大值;(3)先证明PB=PC=BC,在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,当O,E,C′共线时,CE+OE取得最小值.再求其最小值.
(1)证明:在△AOC中,因为OA=OC,D为AC的中点,所以AC⊥DO.
又PO垂直于圆O所在的平面,所以PO⊥AC.
因为DO∩PO=O,所以AC⊥平面PDO.
(2)解:因为点C在圆O上,所以当CO⊥AB时,C到AB的距离最大,且最大值为1.
又AB=2,所以△ABC面积的最大值为![]() .
.
又因为三棱锥P-ABC的高PO=1,
故三棱锥P-ABC体积的最大值为![]() .
.
(3)解:
在△POB中,PO=OB=1,∠POB=90°,
所以![]() .
.
同理![]() ,所以PB=PC=BC.
,所以PB=PC=BC.
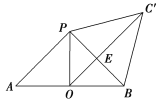
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图所示.
当O,E,C′共线时,CE+OE取得最小值.
又因为OP=OB,![]() ,所以
,所以![]() 垂直平分PB,即E为PB的中点.
垂直平分PB,即E为PB的中点.
从而![]() ,
,
即CE+OE的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知![]() =12sin(x+
=12sin(x+![]() )cosx-3,x∈[o,
)cosx-3,x∈[o,![]() ].
].
(1)求![]() 的最大值、最小值;
的最大值、最小值;
(Ⅱ)CD为△ABC的内角平分线,已知AC=![]() max,BC=
max,BC=![]() ,CD=2
,CD=2![]() ,求∠C.
,求∠C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮.某大学社团调查了该校文学院300名学生每天诵读诗词的时间(所有学生诵读时间都在两小时内),并按时间(单位:分钟)将学生分成六个组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,经统计得到了如图所
,经统计得到了如图所
示的频率分布直方图
(Ⅰ)求频率分布直方图中![]() 的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
(Ⅱ)若两个同学诵读诗词的时间![]() 满足
满足![]() ,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.
,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题的序号有__________.(写出所有真命题的序号)①若![]() ,则“
,则“![]() ”是“
”是“![]() ”成立的充分不必要条件;②命题“
”成立的充分不必要条件;②命题“![]() 使得
使得![]() ”的否定是 “
”的否定是 “![]() 均有
均有![]() ”;③命题“若
”;③命题“若![]() ,则
,则![]() 或
或![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;④函数
”;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
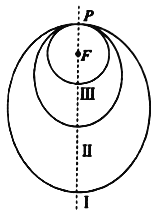
【题目】如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点![]() 变轨进入以月球球心
变轨进入以月球球心![]() 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在![]() 点第二次变轨进入仍以
点第二次变轨进入仍以![]() 为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在
为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在![]() 点第三次变轨进入以
点第三次变轨进入以![]() 为圆心的圆形轨道Ⅲ绕月飞行.已知椭圆轨道Ⅰ和Ⅱ的中心与
为圆心的圆形轨道Ⅲ绕月飞行.已知椭圆轨道Ⅰ和Ⅱ的中心与![]() 在同一直线上,设椭圆轨道Ⅰ和Ⅱ的长半轴长分别为
在同一直线上,设椭圆轨道Ⅰ和Ⅱ的长半轴长分别为![]() ,
,![]() ,半焦距分别为
,半焦距分别为![]() ,
,![]() ,则以下四个关系①
,则以下四个关系①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中正确的是________.
中正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有除颜色外完全相同的黑球和白球共7个,其中白球3个,现有甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时终止.每个球在每一次被取出的机会是等可能的.
(1)求取球2次即终止的概率;
(2)求甲取到白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com