
设数列{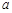 n}满足
n}满足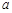 1=
1=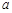 ,
,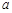 n+1=
n+1=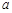 n2+
n2+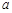 1,
1, .
.
(Ⅰ)当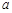 ∈(-∞,-2)时,求证:
∈(-∞,-2)时,求证: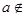 M;
M;
(Ⅱ)当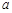 ∈(0,
∈(0,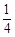 ]时,求证:
]时,求证: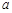 ∈M;
∈M;
(Ⅲ)当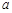 ∈(
∈(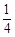 ,+∞)时,判断元素
,+∞)时,判断元素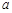 与集合M的关系,并证明你的结论.
与集合M的关系,并证明你的结论.
 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源:设计选修数学-4-5人教A版 人教A版 题型:044
已知函数f(x)=![]() (x≠-1),设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-3|,Sn=b1+b2+…+bn(n∈N+)
(x≠-1),设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-3|,Sn=b1+b2+…+bn(n∈N+)
(1)用数学归纳法证明bn≤![]() ;
;
(2)求证:Sn<![]() .
.
查看答案和解析>>
科目:高中数学 来源:四川省成都石室中学2011届高三“一诊”模拟考试数学理科试题 题型:044
在下表中,每行上的数从左到右都成等比数列,并且所有公比都等于q,每列上的数从上到下都成等差数列,正数aij表示位于第i行第j列的数,其中a24=![]() ,a42=1,a54=
,a42=1,a54=![]() .
.
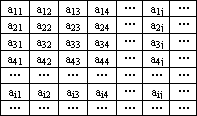
(Ⅰ)求q的值;
(Ⅱ)求aij的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前n项和为Sn,试比较Sn与Tn=![]() (n∈N*)的大小,并说明理由.
(n∈N*)的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:湖北省期中题 题型:解答题
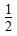 <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小;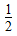 <t<2,bn=
<t<2,bn=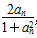 ,求证:
,求证: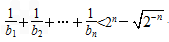
查看答案和解析>>
科目:高中数学 来源:辽宁省沈阳二中2011-2012学年高三上学期10月月考(数学文) 题型:填空题
设数列{an}满足a1=1,3(a1+a2+…+an)=(n+2)an,通项an=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com