
【题目】已知函数![]() .
.![]() ,且
,且![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 与函数
与函数![]() 在公共点
在公共点![]() 处有相同的切线,且
处有相同的切线,且![]() 在
在![]() 上恒成立.
上恒成立.
(i)求![]() 和
和![]() 的值;(
的值;(![]() 为函数
为函数![]() 的导函数)
的导函数)
(ii)求实数n的取值范围.
【答案】(1) 单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 和
和![]() .(2) (i)
.(2) (i)![]() (ii)
(ii)![]()
【解析】
(1)利用导数证明单调性即可;
(2)(i)根据点P是![]() 与
与![]() 的公共点,以及根据导数的几何意义列出方程组,求解即可得到
的公共点,以及根据导数的几何意义列出方程组,求解即可得到![]() 和
和![]() 的值;
的值;
(ii)由![]() ,
,![]() 以及题设条件,判断
以及题设条件,判断![]() 是
是![]() 的极小值点,由
的极小值点,由![]() ,列出方程,构造函数
,列出方程,构造函数![]() ,
,![]() ,利用导数得到其最值,即可得到实数n的取值范围.
,利用导数得到其最值,即可得到实数n的取值范围.
解:(1)∵![]()
又因为![]() ,所以
,所以![]() .
.
令![]() ,则
,则![]() ,
,
∴![]() ;
;
令![]() ,则
,则![]() ,
,
∴![]() 或
或![]()
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 和
和![]() .
.
(2)(i)∵![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线
处有相同的切线
∴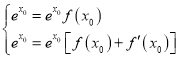 ,∴
,∴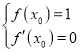 .
.
(ii)∵![]() 在
在![]() 恒成立,且
恒成立,且![]() .
.
![]()
![]() 是
是![]() 的极值点,若
的极值点,若![]() 是
是![]() 的极大值点,由于
的极大值点,由于![]() ,则不满足
,则不满足![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 是
是![]() 的极小值点,由(1)知
的极小值点,由(1)知![]()
∴![]()
∴![]() ,
,![]()
令![]() ,
,![]() ,∴
,∴![]() ,
,
令![]() 则
则![]() ,
,![]() .∵
.∵![]() ,
,![]() ,
,![]() .
.
∴![]() 的值域为
的值域为![]()
所以实数![]() 的取值范围是
的取值范围是![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元),这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据![]() (单位:十亿元).绘制如下表1:
(单位:十亿元).绘制如下表1:
表1
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额 | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示.
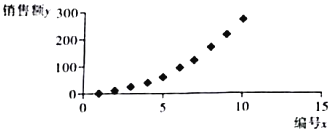
把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为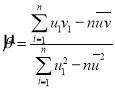 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,(a>b>0)过点(1,
,(a>b>0)过点(1,![]() )且离心率为
)且离心率为![]() .
.
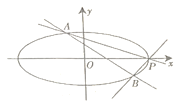
(1)求椭圆C的方程;
(2)设椭圆C的右顶点为P,过定点(2,﹣1)的直线l:y=kx+m与椭圆C相交于异于点P的A,B两点,若直线PA,PB的斜率分别为k1,k2,求k1+k2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Tn为数列{an}的前n项的积,即Tn=a1a2…an.
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=![]() (1﹣an)(n∈N*),证明数列
(1﹣an)(n∈N*),证明数列![]() 为等差数列,并求{an}的通项公式;
为等差数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:
①![]() ;
;
②![]() (1≤k≤99,k∈N*).
(1≤k≤99,k∈N*).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
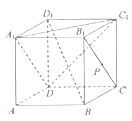
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则 ( )
上运动,则 ( )
A.直线![]() 平面
平面![]()
B.三棱锥![]() 的体积为定值
的体积为定值
C.异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]()
D.直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为![]() 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点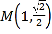 在椭圆上E:
在椭圆上E:![]() (
(![]() ),点
),点![]() 为平面上一点,O为坐标原点.
为平面上一点,O为坐标原点.
(1)当![]() 取最小值时,求椭圆E的方程;
取最小值时,求椭圆E的方程;
(2)对(1)中的椭圆E,P为其上一点,若过点![]() 的直线l与椭圆E相交于不同的两点S和T,且满足
的直线l与椭圆E相交于不同的两点S和T,且满足![]() (
(![]() ),求实数t的取值范围.
),求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com