
分析 (1)由已知及余弦定理可得:$\frac{acosB+bcosA}{c}$=1,可求cosC=$\frac{1}{2}$,结合范围C∈(0,π)可求C的值.
(2)利用三角形面积公式可得ab=8,又a+b=6,利用余弦定理即可求值得解.
解答 解:(1)由余弦定理可得:acosB+bcosA=a×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$+b×$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{2{c}^{2}}{2c}$=c,…3分
∴$\frac{acosB+bcosA}{c}$=1,
∴cosC=$\frac{1}{2}$,
又∵C∈(0,π),C=$\frac{π}{3}$…7分
(2)∵S△ABC=$\frac{1}{2}$absinC=2$\sqrt{3}$,∴ab=8,…10分
又∵a+b=6,
∴c2=a2+b2-2abcosC=(a+b)2-3ab=12,…13分
∴c=2$\sqrt{3}$…14分
点评 本题主要考查了余弦定理,三角形面积公式,特殊角的三角函数值的应用,属于基本知识的考查.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=12x(x>0) | B. | y=0(x<0) | ||
| C. | y2=12x | D. | y2=12x(x>0)或y=0(x<0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一实根 | B. | 至多有一实根 | C. | 没有实根 | D. | 必有唯一的实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
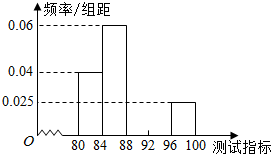 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com