
 对任意函数f(x),x∈D,可按如图所示,构造一个数列发生器,其工作原理如下:
对任意函数f(x),x∈D,可按如图所示,构造一个数列发生器,其工作原理如下:分析 (1)利用f(x)=$\frac{4x-2}{x+1}$,x0=$\frac{49}{65}$及工作原理,注意函数的定义域,直接可求得数列{xn}的只有三项;
(2)要数列发生器产生一个无穷的常数列,则有f(x)=$\frac{4x-2}{x+1}$=x,从而求出相应的初始数据x0的值;
解答 解:(1)∵函数f(x)的定义域D=(-∞,-1)∪(-1,+∞),
∴数列{xn}只有3项,xx=$\frac{11}{19}$,x2=$\frac{1}{5}$,x3=-1.
(2)令f(x)=$\frac{4x-2}{x+1}$=x,即x2-3x+2=0,
解得:x=2,或x=1,
故当x0=2或x0=1时,xn+1=$\frac{4{x}_{n}-2}{{x}_{n}+1}$=xn,
所以,输入的初始数据x0=1时,得到常数列xn=1;
x0=2时,得到常数列xn=2.
点评 本题是数列与算法的简单结合,应搞清算法原理,将问题等价转化,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
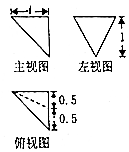
| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀人数 | 非优秀人数 | 总计 | |
| 甲班 | 22 | 8 | 30 |
| 乙班 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 400 | B. | 420 | C. | 440 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{27-n}^{8}$ | B. | A${\;}_{34-n}^{27-n}$ | C. | A${\;}_{34-n}^{7}$ | D. | A${\;}_{34-n}^{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.
在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com