
【题目】如图,ABC为一直角三角形草坪,其中∠C=90°,BC=2米,AB=4米,为了重建草坪,设计师准备了两套方案: 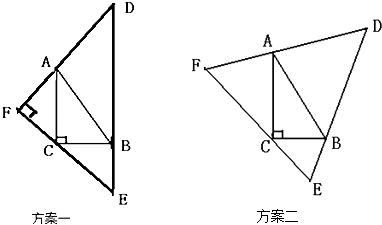
方案一:扩大为一个直角三角形,其中斜边DE过点B,且与AC平行,DF过点A,EF过点C;
方案二:扩大为一个等边三角形,其中DE过点B,DF过点A,EF过点C.
(1)求方案一中三角形DEF面积S1的最小值;
(2)求方案二中三角形DEF面积S2的最大值.
【答案】
(1)解:在方案一:在三角形AFC中,设∠ACF=α,α∈(0, ![]() ),
),
则 ![]() ,
,
因为DE∥AC,所以∠E=α, ![]() ,
,
且 ![]() ,即
,即 ![]() ,
,
解得 ![]() ,
,
所以 ![]() ,
,
所以当sin2α=1,即α=45°时,S1有最小值 ![]()
(2)解:在方案二:在三角形DBA中,设∠DBA=β,β∈(0, ![]() ),则
),则 ![]() ,
,
解得 ![]() ,
,
三角形CBE中,有 ![]() ,解得
,解得 ![]() ,
,
则等边三角形的边长为 ![]()
所以边长的最大值为 ![]() ,所以面积S2的最大值为
,所以面积S2的最大值为 ![]()
【解析】(1)在方案一:在三角形AFC中,设∠ACF=α,α∈(0, ![]() ),表示出三角形DEF面积S1 , 利用基本不等式求出最小值;(2)在方案二:在三角形DBA中,设∠DBA=β,β∈(0,
),表示出三角形DEF面积S1 , 利用基本不等式求出最小值;(2)在方案二:在三角形DBA中,设∠DBA=β,β∈(0, ![]() ),表示出三角形DEF面积S1 , 利用辅助角公式求出最小值.
),表示出三角形DEF面积S1 , 利用辅助角公式求出最小值.
【考点精析】关于本题考查的基本不等式在最值问题中的应用,需要了解用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.单位向量都相等
B.若 ![]() 与
与 ![]() 是共线向量,
是共线向量, ![]() 与
与 ![]() 是共线向量,则
是共线向量,则 ![]() 与
与 ![]() 是共线向量
是共线向量
C.| ![]() +
+ ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]()
![]() =0
=0
D.若 ![]() 与
与 ![]() 是单位向量,则
是单位向量,则 ![]()
![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,点A(1,1),B(0,﹣2),C(4,2),D为AB的中点,DE∥BC. (Ⅰ)求BC边上的高所在直线的方程;
(Ⅱ)求DE所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点与
的一个焦点与![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一顶点为
为对角线的菱形的一顶点为![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式的大小关系正确的是( )
A.sin11°>sin168°
B.sin194°<cos160°
C.tan(﹣ ![]() )<tan(﹣
)<tan(﹣ ![]() )
)
D.cos(﹣ ![]() )>cos
)>cos ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
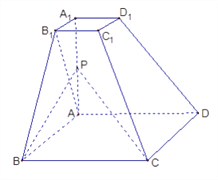
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com