
【题目】已知![]() ,
,![]() .求证:对任意的
.求证:对任意的![]() 都存在A的一个4元分拆:
都存在A的一个4元分拆: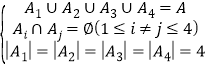 使其中某一个
使其中某一个![]() 的元素恰好是方程
的元素恰好是方程![]() 的一个解.
的一个解.
【答案】见解析
【解析】
依题意,只须证明A中存在4个不同的元素,且某两个之差等于另两个之差.
首先,S中两数之差(大数减小数,以下同)可取1~99共99个值,而A中16个元素可作出![]() 个差.由抽屉原理知,必有2个差是相同的,记为
个差.由抽屉原理知,必有2个差是相同的,记为![]() ,
,
其中![]() ,从而,
,从而,![]() .
.
若![]() ,则命题成立;
,则命题成立;
若![]() ,则取走这一个差
,则取走这一个差![]() (但并不是取走元素
(但并不是取走元素![]() 、
、![]() ),剩下的119个差在1~99之间取值,又必有2个差是相同的,记为
),剩下的119个差在1~99之间取值,又必有2个差是相同的,记为![]() ,其中
,其中![]() ,从而,
,从而,![]() .
.
若![]() ,则命题成立;
,则命题成立;
若![]() ,则取走这一个差
,则取走这一个差![]() ,剩下的118个
,剩下的118个
差在1~99之间取值,又得出必有2个差是相同的.
如此类推,最多进行到第15步时,得出![]() ,其中
,其中![]() ,从而,
,从而,![]() .
.
若![]() ,则命题成立.
,则命题成立.
若![]() ,则前15步积累了15个相同差,
,则前15步积累了15个相同差,
![]() ,①
,①
![]() ,②
,②
……
![]() .
.
由于![]() ,故
,故![]() 不能取A中的最大数也不能取最小数,只有14个可取值,所以,15个
不能取A中的最大数也不能取最小数,只有14个可取值,所以,15个![]() 中必有2个是相同的,不妨设
中必有2个是相同的,不妨设![]() .
.
由于![]() 是在
是在![]() 取走之后才得出的,
取走之后才得出的,
故![]() ,不妨设
,不妨设![]() .
.
①![]() ②得
②得![]() .
.
由![]() ,知
,知![]() ,又
,又![]() ,故
,故![]() ,即
,即![]() 两两不等.
两两不等.
因此,命题成立.
可见,最多进行到第15步时,必能找出A中4个互不相等的元素a、b、c、d,使得![]() .以这4个元素组成
.以这4个元素组成![]() ,便可满足题设的全部条件.
,便可满足题设的全部条件.


科目:高中数学 来源: 题型:
【题目】下列说法中错误的是
①命题“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”;
”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知![]() 为假命题,则实数
为假命题,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④我市某校高一有学生![]() 人,高二有学生
人,高二有学生![]() 人,高三有学生
人,高三有学生![]() 人,现采用分层抽样的方法从该校抽取
人,现采用分层抽样的方法从该校抽取![]() 个学生作为样本进行某项调查,则高三被抽取的学生个数为
个学生作为样本进行某项调查,则高三被抽取的学生个数为![]() 人.
人.
A. ①④ B. ①③④ C. ②④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了坚决打赢新冠状病毒的攻坚战,阻击战,某小区对小区内的![]() 名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取
名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取![]() 名,抽到
名,抽到![]() 岁~
岁~![]() 岁女居民的概率是
岁女居民的概率是![]() .现用分层抽样的方法在全小区抽取
.现用分层抽样的方法在全小区抽取![]() 名居民,则应在
名居民,则应在![]() 岁以上抽取的女居民人数为( )
岁以上抽取的女居民人数为( )
|
|
| |
女生 |
|
|
|
男生 |
|
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,某校学生上学路程所需要时间全部介于![]() 与
与![]() 之间(单位:分钟).现从在校学生中随机抽取
之间(单位:分钟).现从在校学生中随机抽取![]() 人,按上学所学时间分组如下:第
人,按上学所学时间分组如下:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得打如图所示的频率分布直方图.
,得打如图所示的频率分布直方图.
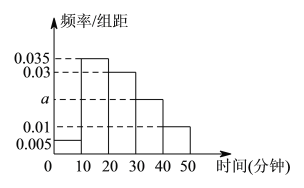
(Ⅰ)根据图中数据求![]() 的值.
的值.
(Ⅱ)若从第![]() ,
,![]() ,
,![]() 组中用分成抽样的方法抽取
组中用分成抽样的方法抽取![]() 人参与交通安全问卷调查,应从这三组中各抽取几人?
人参与交通安全问卷调查,应从这三组中各抽取几人?
(Ⅲ)在(Ⅱ)的条件下,若从这![]() 人中随机抽取
人中随机抽取![]() 人参加交通安全宣传活动,求第
人参加交通安全宣传活动,求第![]() 组至少有
组至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,直线l与椭圆C交于A、B两点,且
,直线l与椭圆C交于A、B两点,且![]()
(1)求椭圆C的方程;
(2)若A、B两点关于原点O的对称点分别为![]() ,且
,且![]() ,判断四边形
,判断四边形![]() 是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郴州市某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表:

(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在![]() 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在![]() 范围内的概率;
范围内的概率;
(3)如果该校以学生对老师评分的中位数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com