练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．化简：$\frac{A_n^m}{{A_{n-1}^{m-1}}}$=n．

    分析 利用排列数公式直接求解．

    解答 解：$\frac{A_n^m}{{A_{n-1}^{m-1}}}$=$\frac{n×（n-1）×（n-2）×…×（n-m+1）}{（n-1）×（n-2）×（n-3）×…×[（n-1）-（m-1）+1]}$=n．
    故答案为：n．

    点评 本题考查排列数公式化简求值，是基础题，解题时要认真审题，注意排列数公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知命题p：已知函数f（x）的定义域为R，若f（x）是奇函数，则f（0）=0，则它的原命题，逆命题、否命题、逆命题中，真命题的个数为（　　）
    A．0B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．一个几何体的三视图如图所示，则该几何体的体积为12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

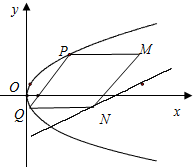    10．抛物线有光学性质，即由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出，反之亦然．如图所示，今有抛物线y2=2px（p＞0），一光源在点M（$\frac{41}{4}$，4）处，由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P，反射后，又射向抛物线上的点Q，再反射后又沿平行于抛物线的轴的方向射出，途中遇到直线l：2x-4y-17=0上的点N，再反射后又射回点M，设P，Q两点的坐标分别是（x1，y1），（x2，y2），
    （Ⅰ）证明：y1y2=-p2；
    （Ⅱ）求抛物线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

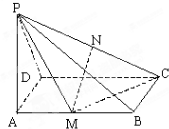    17．如图所示，四棱锥P-ABCD中，底面ABCD是矩形，PA=AD，PA⊥平面ABCD，M、N分别是AB、PC的中点．
    （1）求证：MN∥平面PAD；
    （2）求证：平面PMC⊥平面PCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．公理一：如果一条直线l上的两点A，B在一个平面α内，那么这条直线l在此平面内．请用数学的符号语言表示为A∈l，B∈l，A∈α，B∈α⇒l?α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．函数f（x）=$\frac{\frac{1}{6}•（-1）^{1+{C}_{2x}^{x}}•{A}_{x+2}^{5}}{1+{C}_{3}^{2}+{C}_{4}^{2}+…+{C}_{x-1}^{2}}$ （x∈N）的最大值是-20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若函数f（x）在其定义域上既是减函数又是奇函数，则函数f（x）的解析式可以是（　　）
    A．$f（x）={log_2}（\sqrt{{x^2}+1}-x）$B．$f（x）=\frac{1}{x}$C．f（x）=x2-x3D．f（x）=sinx

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．设在（0，π）内有两个不相等角α，β，满足方程acosx+bsinx+c=0．试证：
    （1）$\frac{a}{cos\frac{α+β}{2}}$=$\frac{b}{sin\frac{α+β}{2}}$=$\frac{c}{cos\frac{α-β}{2}}$；
    （2）cos2$\frac{α-β}{2}$=$\frac{{c}^{2}}{{a}^{2}+{b}^{2}}$．

    查看答案和解析>>

    同步练习册答案