
(本小题满分14分)广东某民营企业主要从事美国的某品牌运动鞋的加工生产,按国际惯例以美元为结算货币,依据以往加工生产的数据统计分析,若加工产品订单的金额为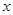 万美元,可获得加工费近似为
万美元,可获得加工费近似为 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失 万美元,其中
万美元,其中 为该时段美元的贬值指数,
为该时段美元的贬值指数,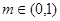 ,从而实际所得的加工费为
,从而实际所得的加工费为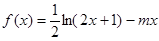 (万美元).
(万美元).
(Ⅰ)若某时期美元贬值指数 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随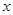 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额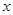 应在什么范围内?
应在什么范围内?
(Ⅱ)若该企业加工产品订单的金额为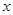 万美元时共需要的生产成本为
万美元时共需要的生产成本为 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为 (其中
(其中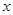 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.
(Ⅰ)加工产品订单的金额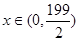 ,该企业实际所得加工费随
,该企业实际所得加工费随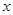 的增加而增加.
的增加而增加.
(Ⅱ)当美元的贬值指数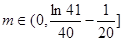 时,该企业加工生产不会亏损.
时,该企业加工生产不会亏损.
解析试题分析:(I)当 时,
时, ,然后求导根据导数大于零求得x的取值范围.
,然后求导根据导数大于零求得x的取值范围.
(II)搞清本小题不会出现亏损,也就是当 时,都有
时,都有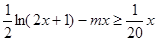 ,即
,即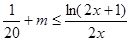 恒成立,然后构造函数
恒成立,然后构造函数 ,利用导数研究它的最小值即可.
,利用导数研究它的最小值即可.
(Ⅰ)由已知 得:
得: ,其中
,其中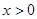
所以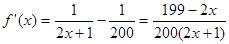 ,由
,由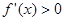 ,即
,即 ,
,
解得
即加工产品订单的金额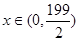 ,该企业实际所得加工费随
,该企业实际所得加工费随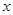 的增加而增加.
的增加而增加.
··································· 5分
(Ⅱ)依题设企业加工生产将不会出现亏损,则当 时,都有
时,都有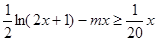 ,······················· 7分
,······················· 7分
由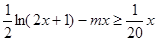 得:
得: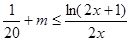
令 ,则
,则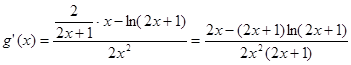 ·········· 8分
·········· 8分
令 ,则
,则 ········ 10分
········ 10分
可知 在
在 上单调递减,从而
上单调递减,从而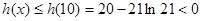 ,··· 11分
,··· 11分
所以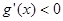 ,可知
,可知 在
在 上单调递减,因此
上单调递减,因此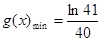 ,即
,即 13分
13分
故当美元的贬值指数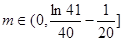 时,该企业加工生产不会亏损. 14分
时,该企业加工生产不会亏损. 14分
考点: 数学模型的建立,导数在求最值,单调区间中的应用.
点评:本小题关键是理解实际问题当中的要求如何通过数学方法实现,如企业实际所得加工费随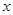 的增加而增加本质就是求函数f(x)的单调增区间.企业加工生产将不会出现亏损本质就是当
的增加而增加本质就是求函数f(x)的单调增区间.企业加工生产将不会出现亏损本质就是当 时,不等式
时,不等式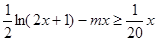 恒成立问题.
恒成立问题.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
商店出售茶壶和茶杯,茶壶单价为每个20元,茶杯单价为每个5元,该店推出两种促销优惠办法:
(1)买1个茶壶赠送1个茶杯;
(2)按总价打9.2折付款。
某顾客需要购买茶壶4个,茶杯若干个,(不少于4个),若设购买茶杯数为x个,付款数为y(元),试分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更省钱?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品在近30天内每天的销售价格P(元)与时间t(天)的函数关系式为:
P=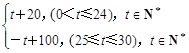 ;该商品的日销售量Q(件)与时间(天)的函数关系式为:
;该商品的日销售量Q(件)与时间(天)的函数关系式为:
Q=-t+40(0<t≤30,t∈N*).求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知26辆货车以相同速度v由A地驶向400千米处的B地,每两辆货车间距离为d千米,现已知d与v的平方成正比,且当v=20(千米/时)时,d=1(千米).
(1)写出d与v的函数关系;
(2)若不计货车的长度,则26辆货车都到达B地最少需要多少小时?此时货车速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com