
分析 (1)利用诱导公式化简极限是的解析式,代入求值即可.
(2)利用函数的解析式化简,求出余弦函数,然后求解即可.
(3)求出正切函数值,然后化简所求的表达式为正切函数的形式,代入求解即可.
解答 解:(1)f(α)=$\frac{sin(π-α)•cos(2π-α)•sin(-α+\frac{3π}{2})}{cos(-π-α)•cos(-α+\frac{3π}{2})}$
=$\frac{-sinα•cosα•cosα}{cosα•sinα}$=-cosα.
f(-$\frac{31π}{3}$)=-cos($-\frac{31π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$.
(2)f(α)=$\frac{3}{5}$,可得cosα=-$\frac{3}{5}$,∴sinα=±$\frac{4}{5}$,tanα=±$\frac{4}{3}$.
(3)2f(π+α)=f($\frac{π}{2}$+α),
可得-2cos(π+α)=-cos($\frac{π}{2}$+α)=sinα,可得tanα=2.
$\frac{sinα+cosα}{sinα-cosα}$+cos2α=$\frac{tanα+1}{tanα-1}$+$\frac{1}{{tan}^{2}α+1}$=3+$\frac{1}{5}$=$\frac{16}{5}$.
点评 本题考查诱导公式的应用,三角函数的化简求值,同角三角函数的基本关系式的应用,考查计算能力.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
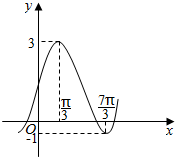 已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
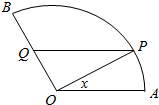 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | -32 | C. | 256 | D. | -256 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com