
【题目】已知点![]() 在椭圆
在椭圆![]() 上,动点
上,动点![]() 都在椭圆上,且直线
都在椭圆上,且直线![]() 不经过原点
不经过原点![]() ,直线
,直线![]() 经过弦
经过弦![]() 的中点.
的中点.
(1)求椭圆![]() 的方程和直线
的方程和直线![]() 的斜率;
的斜率;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】试题分析:(1)将![]() 代入
代入![]() ,得
,得![]() ,可得椭圆方程为
,可得椭圆方程为![]() ,设直线
,设直线![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() 由
由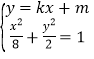 得
得![]() ,根据韦达定理及斜率公式可得
,根据韦达定理及斜率公式可得![]() ;(2)由弦长公式及三角形面积公式可得
;(2)由弦长公式及三角形面积公式可得![]() 面积
面积![]()
![]() ,利用导数可求得
,利用导数可求得![]() 面积的最大值.
面积的最大值.
试题解析:(1)将![]() 代入
代入![]() ,得,
,得,
![]() ,
,![]() ,
,
椭圆方程为![]()
设直线![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]()
由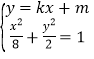 得
得![]()
![]() ,
,![]() ,
,
直线![]() 经过弦
经过弦![]() 的中点,则
的中点,则![]() ,
,![]() ,
,
![]() ,
,![]()
(2)当![]() 时,由
时,由![]() 得
得![]() ,
,![]() ,
,![]()
![]()
![]()
点![]() 到直线
到直线![]() 的距离
的距离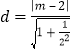 ,
,
![]() 面积
面积![]()
![]()
设![]() ,
,
则![]()
![]()
求得![]() ,所以
,所以![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用导数研究函数的单调性,从而求得求三角形面积最大值的.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为![]() 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留
平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留![]() 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为
米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为![]() 米,如图所示.
米,如图所示.

(1)将两个养殖池的总面积![]() 表示
表示![]() 为的函数,并写出定义域;
为的函数,并写出定义域;
(2)当温室的边长![]() 取何值时,总面积
取何值时,总面积![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com