
科目: 来源: 题型:解答题
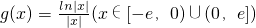 ,求证:当a=-1时,
,求证:当a=-1时,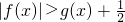 .
.查看答案和解析>>
科目: 来源: 题型:解答题
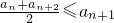 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.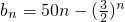 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围;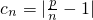 (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:单选题
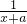 >0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案:
>0恒成立,求实数a的取值范围.”有两位同学用数形结合的方法分别提出了自己的解题思路和答案: 和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]
和g(x)=-x+a的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在g(x)的上方.可解得a的取值范围是[0,+∞]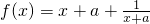 的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].
的大致图象,随着a的变化,要求f(x)的图象再y轴右侧的部分恒在直线y=2a的上方.可解得a的取值范围是[0,1].查看答案和解析>>
科目: 来源: 题型:解答题
 时,令h(x)=f′(x)+6x,求证:当x∈(0,+∞)时,h(x)≥2elnx(e为自然对数的底数.)
时,令h(x)=f′(x)+6x,求证:当x∈(0,+∞)时,h(x)≥2elnx(e为自然对数的底数.)查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com