
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.
如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2}{3}$π | D. | $\frac{5}{6}$π或$\frac{π}{6}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
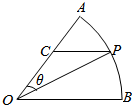 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com