练习册

  • 练习册
  • 试题
    相关习题
     0  251424  251432  251438  251442  251448  251450  251454  251460  251462  251468  251474  251478  251480  251484  251490  251492  251498  251502  251504  251508  251510  251514  251516  251518  251519  251520  251522  251523  251524  251526  251528  251532  251534  251538  251540  251544  251550  251552  251558  251562  251564  251568  251574  251580  251582  251588  251592  251594  251600  251604  251610  251618  266669 

    科目： 来源： 题型：选择题

    15．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+3x（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，则f（g（-1））=（　　）
    A．-28B．-8C．-4D．4

    查看答案和解析>>

    科目： 来源： 题型：选择题

    14．在下列给出的命题中，所有正确命题的个数为（　　）
    ①函数y=2x3-3x+1的图象关于点（0，1）成中心对称；
    ②对?x，y∈R，若x+y≠0，则x≠1或y≠-1；
    ③若实数x，y满足x2+y2=1，则$\frac{y}{x+2}$的最大值为$\frac{\sqrt{3}}{3}$；
    ④若△ABC为锐角三角形，则sinA＜cosB．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目： 来源： 题型：填空题

    13．下列四个命题：①?x0∈R，使sinx0+cosx0=2；②对?x∈R，sinx+$\frac{1}{sinx}$≥2；③对?x∈（0，$\frac{π}{2}$），tanx+$\frac{1}{tanx}$≥2；④?x0∈R，使sinx0+cosx0=$\sqrt{2}$．其中正确命题的序号为③④．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．函数y=sin（ωx+φ）（ω＞0且|φ＜|$\frac{π}{2}$）在区间[$\frac{1}{12}$，$\frac{7}{12}$]上单调递减，且函数值从1减小到-1，那么此函数图象与y轴交点的纵坐标为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{6}+\sqrt{2}}{4}$

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．下列说法中错误的是（　　）
    A．对于命题p：?x0∈R，使得x0+$\frac{1}{{x}_{0}}$＞2，则￢p：?x∈R，均有x+$\frac{1}{x}$≤2
    B．“x=1”是“x2-3x+2=0”的充分不必要条件
    C．命题“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0”
    D．若p∧q为假命题，则p，q均为假命题

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．已知函数f（x）=sin（ωx+$\frac{π}{6}$）（ω＞0）的最小正周期为π，则该函数的图象（　　）
    A．关于直线x=$\frac{π}{6}$对称B．关于直线x=$\frac{π}{4}$对称．
    C．关于点（$\frac{π}{4}$，0）对称D．关于点（$\frac{π}{6}$，0）对称

    查看答案和解析>>

    科目： 来源： 题型：填空题

    9．如图是一个空间几何体的三视图，则这个几何体的外接球的体积是$\frac{125\sqrt{2}}{3}π$cm3．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．已知M={x|x2+x-2＞0}，$N=\{x|\frac{2}{2-x}＞1\}$，则M∩N=（　　）
    A．{x|1＜x＜2}B．{x|0＜x＜1}C．{x|x＜-2或x＞1}D．{x|-2＜x＜2}

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．已知双曲线C的中心在原点，焦点在x轴上，离心率为$\sqrt{2}$，且经过点$（4，-\sqrt{10}）$．
    （Ⅰ）求双曲线C的方程；
    （Ⅱ）求双曲线的顶点坐标，焦点坐标，渐近线方程．

    查看答案和解析>>

    科目： 来源： 题型：解答题

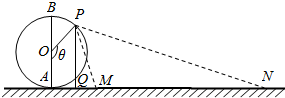    6．如图，摩天轮的半径OA为50m，它的最低点A距地面的高度忽略不计．地面上有一长度为240m的景观带MN，它与摩天轮在同一竖直平面内，且AM=60m．点P从最低点A处按逆时针方向转动到最高点B处，记∠AOP=θ，θ∈（0，π）．
    （Ⅰ）当θ=$\frac{2π}{3}$ 时，求点P距地面的高度PQ；
    （Ⅱ）设y=tan∠MPN，写出用θ表示y的函数关系式，并求y的最大值．

    查看答案和解析>>

    同步练习册答案