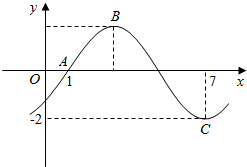14．已知函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
（1）写出函数f（x）的最小正周期及其单调递减区间；
（2）求f（x）的解析式；
（3）若将函数f（x）的图象平移Φ个单位，得到一个偶函数的图象，求|Φ|的最小值；
（4）求函数y=f（x-3）+f（2x+7）（x∈[0，2]）的值域．

13．已知正方体ABCD-A₁B₁C₁D₁，底面ABCD的中心为O，E为A₁B₁中点，F为CC₁中点，如图．
（1）求证：A₁O⊥BD；
（2）求证：A₁O⊥平面BDF；
（3）求证：平面AD₁E⊥平面ACD₁．

12．某个公司调查统计它的员工每周参与体育锻炼的时间，样本容量为100人，将调查结果统计为频率分布直方图，如图．我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”，并将有关性别的信息统计到表中．

	“勤于锻炼者”	非“勤于锻炼者”	合计
男	25		70
女
合计

（1）根据图表信息，判断“勒于锻炼者”是否与性别有关？
附：X²=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}+{n}_{+2}}$

p（X2≥k）	0.05	0.01
k	3.841	6.635

（2）在调查中还统计了员工的年龄，发现公司员工的年龄服从正态分布N（35，9），那么从公司中随机选取一名员工，他的年龄在32-38岁之间的概率是多少？（Φ（1）=0.8413）
（3）由于猜测员工的锻炼时间y与年龄x成线性相关，所以根据调查结果进行了线性回归分析，得到回归方程为y=-5x+b，如果员工的平均锻炼时间是110分钟，那么请判断下列说法的正误：
①b=285；
②由于回归方程的斜率是负的，说明年龄越大的员工，每周锻炼时间一定越短；
③由于回归直线方程的斜率是负的，说明两个变量的相关关系是负相关；
④能够算出回归方程，说明两个变旦之间确实是线性相关关系；
⑤回归直线是所有直线中穿过数据点最多的直线；
⑥两个变量是不是成线性相关关系还要看相关系数的大小．

11．某个停车场有一排共12个车位，从入口开始依次编号是1号停车位、2号停车位、…、12号停车位．早上来了8辆车，随机地停在了其中8个车位．
（1）这时有一辆体型较大的工程车到达停车场，它需要占据两个相邻的车位，求工程车能停进车位的概率；
（2）求没有三辆车相邻的概率；
（3）如果有4辆车离开之后，又有一辆车开进来，停在离入口最近的空车位，记这个车位的编号是η，求η的期望．

10．n∈N^*，证明不等式：$\frac{2-1}{{2}^{2}-1}$+$\frac{{2}^{2}-1}{{2}^{3}-1}$+…+$\frac{{2}^{n}-1}{{2}^{n+1}-1}$＞$\frac{n}{2}$-$\frac{1}{3}$．

9．求由抛物线y=x²-2x+5与直线y=x+5所围成的图形的面积S．

8．已知函数f（x）=$\frac{-{2}^{x}+b}{{2}^{x+1}+a}$在实数集R上定义，a，b是方程${5}^{{x}^{2}-3x+1}=\frac{1}{5}$的实根，且a＞b．
（1）求a，b的值；
（2）判断函数f（x）的奇偶性；
（3）证明函数f（x）在R上是减函数；
（4）若对任意的实数t，不等式f（t²-2t）+f（2t²-k）＜0恒成立，求k的取值范围．

7．已知函数f（x）的图象关于y轴对称，且满足f（1+x）=f（1-x），当x∈[0，1]时，f（x）=x²，则函数f（x）在R上的解析式是f（x）=（x-2k）²，x∈[2k-1，2k+1]，k∈Z，函数y=f（x）-log₃x的零点有4个．

6．在平面直角坐标系中，以原点为极点，x轴的非负半轴为极轴建立极坐标系，点P的极坐标为（2，$\frac{π}{6}$），曲线C的极坐标方程为ρ²+2ρsinθ=3．
（1）写出点P的直角坐标及曲线C的直角坐标方程；
（2）若Q为C上的动点，求PQ的中点M到直线l：$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=3+\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数）距离的最大值．

5．满足A₁∪A₂={x，y，z}的有序集合对（A₁，A₂）的个数是（　　）

A．

6

B．

8

C．

24

D．

27