
科目: 来源:2017届贵州遵义南白中学高三联考二数学(理)试卷(解析版) 题型:选择题
如图,已知双曲线
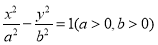 的左、右焦点分别为
的左、右焦点分别为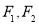 ,离心率为2,以双曲线
,离心率为2,以双曲线 的实轴为直径的圆记为圆
的实轴为直径的圆记为圆 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 ,则以
,则以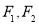 为焦点,过点
为焦点,过点 的椭圆
的椭圆 的离心率为( )
的离心率为( )
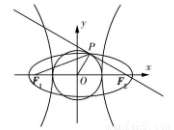
A.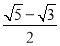 B.
B.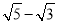 C.
C. D.
D.
查看答案和解析>>
科目: 来源:2017届贵州遵义南白中学高三联考二数学(理)试卷(解析版) 题型:选择题
已知函数 是定义在
是定义在 上的奇函数,对任意两个不相等的正数
上的奇函数,对任意两个不相等的正数 ,都有
,都有 ,记
,记 ,
,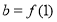 ,
,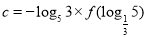 ,则( )
,则( )
A. B.
B.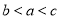 C.
C. D.
D.
查看答案和解析>>
科目: 来源:2017届贵州遵义南白中学高三联考二数学(理)试卷(解析版) 题型:解答题
十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为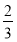 ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为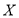 ,求
,求 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
查看答案和解析>>
科目: 来源:2017届贵州遵义南白中学高三联考二数学(理)试卷(解析版) 题型:解答题
已知矩形 中,
中, ,
, 分别在
分别在 上,且
上,且 ,沿
,沿 将四边形
将四边形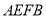 折成四边形
折成四边形 ,使点
,使点 在平面
在平面 上的射影
上的射影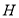 在直线
在直线 上,且
上,且 .
.

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源:2017届贵州遵义南白中学高三联考二数学(理)试卷(解析版) 题型:解答题
已知椭圆
 过点
过点 ,离心率为
,离心率为 ,
, 分别为左右焦点.
分别为左右焦点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 上存在两个点
上存在两个点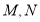 ,椭圆上有两个点
,椭圆上有两个点 满足
满足 三点共线,
三点共线, 三点共线,且
三点共线,且 ,求四边形
,求四边形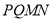 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com