
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
已知等比数列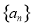 单调递增,记数列
单调递增,记数列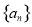 的前
的前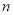 项之和为
项之和为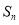 ,且满足条件
,且满足条件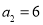 ,
,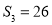 .
.
(1)求数列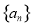 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前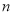 项之和
项之和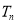 .
.
查看答案和解析>>
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知 、
、 ,
, 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求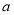 ,
, 的值;
的值;
(2)该电子商务平台将年龄在 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
已知四棱柱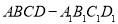 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且 ,
,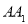 ⊥平面
⊥平面 ,
,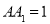 ,设
,设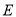 为
为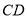 的中点.
的中点.

(1)求证: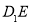 ⊥平面
⊥平面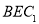 ;
;
(2)点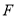 在线段
在线段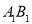 上,且
上,且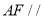 平面
平面 ,求平面
,求平面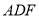 和平面
和平面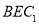 所成锐角的余弦值.
所成锐角的余弦值.
查看答案和解析>>
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
已知椭圆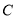 :
: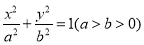 的离心率为
的离心率为 ,椭圆
,椭圆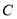 和抛物线
和抛物线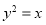 交于
交于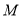 ,
,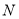 两点,且直线
两点,且直线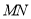 恰好通过椭圆
恰好通过椭圆 的右焦点.
的右焦点.
(1)求椭圆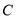 的标准方程;
的标准方程;
(2)经过椭圆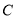 右焦点的直线
右焦点的直线 和椭圆
和椭圆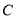 交于
交于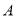 ,
, 两点,点
两点,点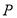 在椭圆上,且
在椭圆上,且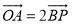 ,其中
,其中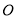 为坐标原点,求直线
为坐标原点,求直线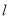 的斜率.
的斜率.
查看答案和解析>>
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
已知函数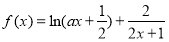 .
.
(1)若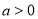 ,且
,且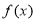 在
在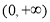 上单调递增,求实数
上单调递增,求实数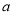 的取值范围;
的取值范围;
(2)是否存在实数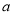 ,使得函数
,使得函数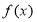 在
在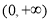 上的最小值为1?若存在,求出实数
上的最小值为1?若存在,求出实数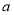 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2017届重庆市高三上期中数学(理)试卷(解析版) 题型:解答题
在直角坐标系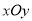 中,曲线
中,曲线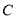 的参数方程为
的参数方程为 (
(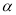 为参数).
为参数).
(1)求曲线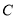 的普通方程;
的普通方程;
(2)在以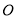 为极点,
为极点,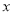 正半轴为极轴的极坐标系中,直线
正半轴为极轴的极坐标系中,直线 方程为
方程为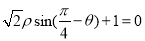 ,已知直线
,已知直线 与曲线
与曲线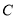 相交于
相交于 ,
,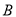 两点,求
两点,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com