
科目: 来源: 题型:
【题目】中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜),进入总决赛的甲乙两队中,若每一场比赛甲队获胜的概率为![]() ,乙队获胜的概率为
,乙队获胜的概率为![]() ,假设每场比赛的结果互相独立,现已赛完两场,乙队以2:0暂时领先.
,假设每场比赛的结果互相独立,现已赛完两场,乙队以2:0暂时领先.
(1)求甲队获得这次比赛胜利的概率;
(2)设比赛结束时两队比赛的场数为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是枣强县普通职工
是枣强县普通职工![]() (
(![]() ,
,![]() )个人的年收入,设
)个人的年收入,设![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增加,中位数一定变大,方差可能不变
B.年收入平均数大大增加,中位数可能不变,方差变大
C.年收入平均数大大增加,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=(x﹣a)2lnx,a∈R.
(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)﹣4e2只有一个零点,求实数a的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}是公差为3的等差数列,数列{bn}是b1=1的等比数列,且![]() .
.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
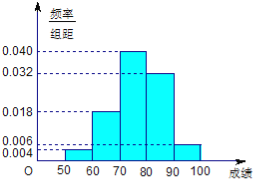
【题目】某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
性别与读营养说明列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(Ⅰ)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(Ⅱ)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:![]() ,其中
,其中![]() 为样本容量.)
为样本容量.)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,左、右顶点分别为
的焦距为2,左、右顶点分别为![]() ,
,![]() 是椭圆上一点,记直线
是椭圆上一点,记直线![]() 的斜率为
的斜率为![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆经过原点,且线段
为直径的圆经过原点,且线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.

(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(1)求男生成绩的中位数及女生成绩的平均值;
(2)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com