
科目: 来源: 题型:
【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
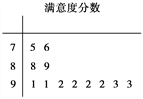
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的分别列和期望;
的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,利用简单随机抽样的方法在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前n项和为Sn,点
的前n项和为Sn,点![]() 在直线
在直线![]() 上,数列
上,数列![]() 为等差数列,且
为等差数列,且![]() ,前9项和为153.
,前9项和为153.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求使不等式
,求使不等式![]() 对一切的
对一切的![]() 都成立的最大整数k.
都成立的最大整数k.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的图象在点
)的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函数![]() 的表达式;
的表达式;
(2)设函数![]() (
(![]() )的两个极值点
)的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点.当
的零点.当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC,四边形BB1C1C为正方形,设AB1的中点为D,B1C∩BC1=E.
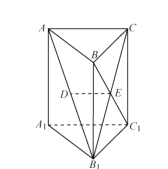
求证:(1)DE∥平面AA1C1C;
(2)BC1⊥平面AB1C.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,
其中![]() ,若函数
,若函数![]() ,且它的最小正周期为
,且它的最小正周期为![]() .
.
(普通中学只做1,2问)
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() (其中
(其中![]() )时,记函数
)时,记函数![]() 的最大值与最小值分
的最大值与最小值分
别为![]() 与
与![]() ,设
,设![]() ,求函数
,求函数![]() 的解
的解
析式;
(3)在第(2)问的前提下,已知函数![]() ,
, ![]() ,若对于任意
,若对于任意![]() ,
, ![]() ,总存在
,总存在![]() ,使得
,使得![]()
![]() 成立,求实数t的取值范围.
成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com