
科目: 来源: 题型:
【题目】定义:在数列![]() 中,若
中,若![]() 为常数)则称
为常数)则称![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若![]() 是“等方差数列”,在数列
是“等方差数列”,在数列![]() 是等差数列;
是等差数列;
②![]() 是“等方差数列”;
是“等方差数列”;
③若![]() 是“等方差数列”,则数列
是“等方差数列”,则数列![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
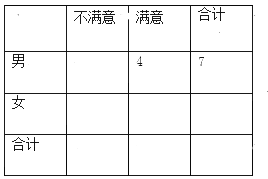
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得![]() ,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?

附:

(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如表所示:

(1)作出散点图;
(2)如果![]() 与
与![]() 线性相关,求出回归直线方程.
线性相关,求出回归直线方程.
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,
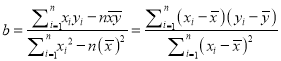 ,
, ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地自来水苯超标,当地自来水公司对水质检测后,决定在水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中 ,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为![]() ,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com