
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.
的值;若不存在,请说理由.
(参考数据: ![]() ,
, ![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=aln x+![]() (a∈R).
(a∈R).
(1)当a=1时,求f(x)在x∈[1,+∞)内的最小值;
(2)若f(x)存在单调递减区间,求a的取值范围;
(3)求证ln(n+1)> ![]() +
+![]() +
+![]() +…+
+…+![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】等比数列{an}的前n项和为Sn,已知对任意的n∈N*,点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图象上.
(1)求r的值;
(2)当b=2时,记bn=2(log2an+1)(n∈N*),证明:对任意的n∈N*,不等式![]() ·
·![]() ·…·
·…·![]() >
>![]() 成立.
成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
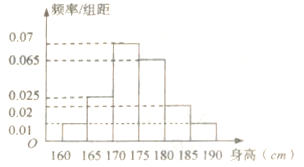
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足a1=a,an+1=2an+![]() (a,λ∈R).
(a,λ∈R).
(1)若λ=-2,数列{an}单调递增,求实数a的取值范围;
(2)若a=2,试写出an≥2对任意的n∈N*成立的充要条件,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P
=1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P![]() .
.
(1)求椭圆C的离心率;
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且![]() =
=![]() +
+![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com