
科目: 来源: 题型:
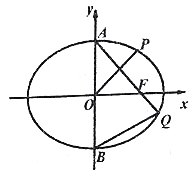
【题目】如图,椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,
, ![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .
.
(1)若点![]() 坐标为
坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)延长![]() 交椭圆
交椭圆![]() 与点
与点![]() ,若直线
,若直线![]() 的斜率是直线
的斜率是直线![]() 的斜率的3倍,求椭圆
的斜率的3倍,求椭圆![]() 的离心率;
的离心率;
(3)是否存在椭圆![]() ,使直线
,使直线![]() 平分线段
平分线段![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
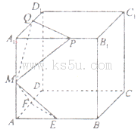
【题目】已知棱长为l的正方体![]() 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、![]() 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段![]() 上,且
上,且![]() ,设面
,设面![]() 面MPQ=
面MPQ=![]() ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,![]() 不是定直线
不是定直线
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知c=2,C=![]() .
.
(1)若△ABC的面积等于![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

![]() .
. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为![]()
![]() ,设圆柱的高度为
,设圆柱的高度为![]()
![]() ,底面半径为
,底面半径为![]()
![]() ,且
,且![]() .假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元/
元/ ![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元/
元/ ![]() (
(![]() ,
, ![]() 为常数,且
为常数,且![]() ).
).

(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
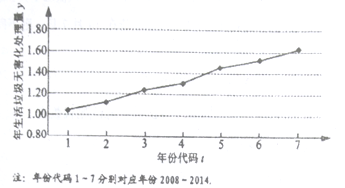
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
参考数据: ![]() ,
, ![]() ,
, 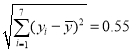 ,
, ![]() .
.
参考公式:相关系数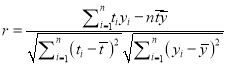
回归方程![]() 中,
中, 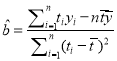 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com