
科目: 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
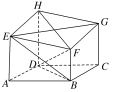
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)=![]() ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=![]() .
.
(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
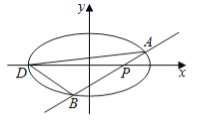
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图,在多面体![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
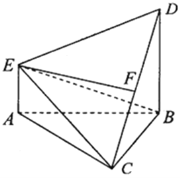
(1)若![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() (
(![]() ﹥
﹥![]() ﹥0)的离心率为
﹥0)的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com