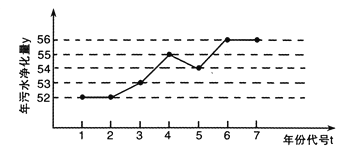
注: 年份代码1-7分别对应年份2010-2016.

（1）由折线图看出，可用线性回归模型拟合和的关系，请用相关系数加以说明；

（2）建立关于的回归方程，预测年该企业污水净化量；

（3）请用数据说明回归方程预报的效果.

附注: 参考数据:；

参考公式：相关系数，回归方程中斜率和截距的最小；

二乘法估汁公式分别为；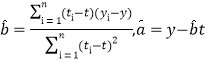

反映回归效果的公式为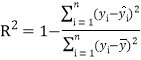：，其中越接近于，表示回归的效果越好.

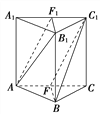
求证：(1)平面AB1F1∥平面C1BF；

(2)平面AB1F1⊥平面ACC1A1.

（1）指出这组数据的众数和中位数；

（2）若幸福度不低于9．5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；

（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记表示抽到“极幸福”的人数，求的分布列及数学期望．

【题目】为响应阳光体育运动的号召，某县中学生足球活动正如火如荼地展开，该县为了解本县中学生的足球运动状况，根据性别采取分层抽样的方法从全县24000名中学生（其中男生14000人，女生10000人）中抽取120名，统计他们平均每天足球运动的时间，如下表：（平均每天足球运动的时间单位为小时，该县中学生平均每天足球运动的时间范围是）.

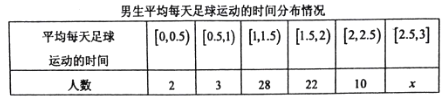
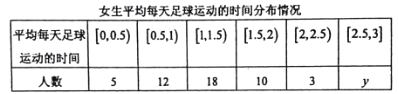
（1）请根据样本估算该校男生平均每天足球运动的时间（结果精确到0.1）；

（2）若称平均每天足球运动的时间不少于2小时的学生为“足球健将”，低于2小时的学生为“非足球健将”.

①请根据上述表格中的统计数据填写下面列联表，并通过计算判断，能否有90%的把握认为是否为“足球健将”与性别有关？

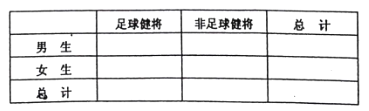
②若在足球运动时间不足1小时的男生中抽取2名代表了解情况，求这2名代表都是足球运动时间不足半小时的概率.

参考公式：，其中.

参考数据：

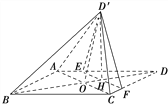
(1)证明：AC⊥HD′；

(2)若AB＝5，AC＝6，AE＝，OD′＝2，求五棱锥D′ABCFE的体积．

A. AC B. BD C. A1D D. A1A

(1)共有几种放法？

(2)恰有1个空盒，有几种放法？

(3)恰有2个盒子不放球，有几种放法？

【题目】某少数民族的刺绣有着悠久的历史，下图为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含个小正方形.

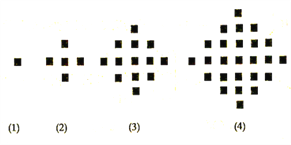
（1）求出；

（2）利用合情推理的“归纳推理思想”归纳出与的关系式，

（3）根据你得到的关系式求的表达式

【题目】已知直线与函数的图像相切于点．

（1）求实数的值；

（2）证明除切点外，直线总在函数的图像的上方；

（3）设是两两不相等的正实数，且成等比数列，试判断与的大小关系，并证明你的结论．

【题目】随着机构改革工作的深入进行，各单位要减员增效，有一家公司现有职员2a人(140<2a<420，且a为偶数)，每人每年可创利b万元．据评估，在经营条件不变的前提下，每裁员1人，则留岗职员每人每年多创利0.01b万元，但公司需付下岗职员每人每年0.4b万元的生活费，并且该公司正常运转所需人数不得小于现有职员的，为获得最大的经济效益，该公司应裁员多少人？