
科目: 来源: 题型:
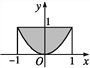
【题目】利用随机模拟方法计算y=x2与y=4围成的面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换,a=4a1-2,b=4b1,试验进行100次,前98次中落在所求面积区域内的样本点数为65,已知最后两次试验的随机数a1=0.3,b1=0.8及a1=0.4,b1=0.3,那么本次模拟得出的面积的近似值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设![]() 分别表示5名学生分配到王城公园和牡丹公园的人数,记
分别表示5名学生分配到王城公园和牡丹公园的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”(【注】三升九:3.9升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目: 来源: 题型:
【题目】经市场调查,某商品在过去的20天内的价格![]() (单位:元)与销售量
(单位:元)与销售量![]() (单位:件)均为时间
(单位:件)均为时间![]() (单位:天)的函数,且价格满足
(单位:天)的函数,且价格满足![]() ,销售量满足
,销售量满足![]() ,其中
,其中![]() ,
, ![]() .
.
(1)请写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)求该商品的日销售额的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若函数![]() ,
, ![]() 的最小值为-16,求实数
的最小值为-16,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
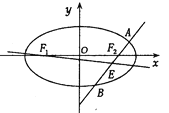
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=4cosθ,直线![]() 的参数方程为:
的参数方程为:  (t为参数),两曲线相交于M,N两点.
(t为参数),两曲线相交于M,N两点.
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)若P(﹣2,﹣4),求|PM|+|PN|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com