
科目: 来源: 题型:
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为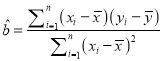 ,
, ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解某地区心肺疾病是否与性别有关,在某医院随机地对入院
的50人进行了问卷调查,得到了如下的![]() 列联表:
列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽取6人,其中男性抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,判断是否有
,判断是否有![]() 的把握认为
的把握认为
患心肺疾病与性别有关?
右面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 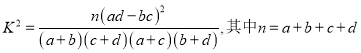 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 是否满足
是否满足![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题。”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论。现从该班随机抽取5位学生在一次考试中的数学和物理成绩,如下表:

(1)求数学成绩y对物理成绩x的线性回归方程![]() 。若某位学生的物理成绩为80分,预测他的数学成绩;
。若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这5位学生中随机抽取2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率。(参考公式: 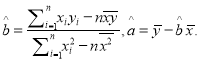 参考数据:
参考数据: ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三数学竞赛初赛考试后,对部分考生的成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,若第四、五、六组的人数依次成等差数列,且第六组有4人.

(1)请补充完整频率分布直方图,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为![]() .若
.若![]() ,则称此二人为“黄金帮扶组”.试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”.试求选出的二人为“黄金帮扶组”的概率![]() ;
;
(3)以此样本的频率当做概率,现随机在这所有考生中选出3名学生,求成绩不低于120分的人数![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com