
科目: 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
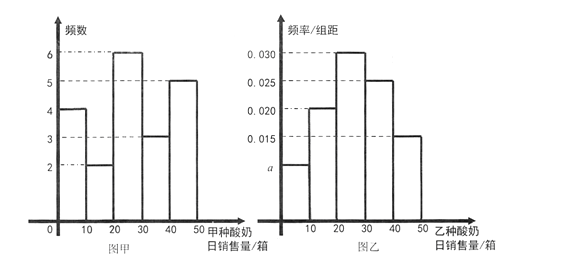
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() .
.
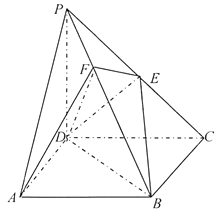
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
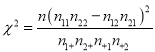
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.
年龄 分组 | 抽取份数 | 答对全卷 的人数 | 答对全卷的人数 占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) |
| 27 | 0.9 |
[40,50) | 10 | 4 |
|
[50,60] | 20 |
| 0.1 |

(1)分别求出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取2人授予“环保之星”,求年龄在
答对全卷的人中随机抽取2人授予“环保之星”,求年龄在![]() 的人中至少有1人被授予“环保之星”的概率.
的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合![]() .对于
.对于![]() ,
, ![]() ,定义
,定义![]() 与
与![]() 之间的距离为
之间的距离为![]() .
.
(Ⅰ)写出![]() 中的所有元素,并求两元素间的距离的最大值;
中的所有元素,并求两元素间的距离的最大值;
(Ⅱ)若集合![]() 满足:
满足: ![]() ,且任意两元素间的距离均为2,求集合
,且任意两元素间的距离均为2,求集合![]() 中元素个数的最大值并写出此时的集合
中元素个数的最大值并写出此时的集合![]() ;
;
(Ⅲ)设集合![]() ,
, ![]() 中有
中有![]() 个元素,记
个元素,记![]() 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为![]() ,证明
,证明![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点P (3, ![]() )且倾斜角为
)且倾斜角为![]() .在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
.在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求直线l的一个参数方程和圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B,求![]() 的值.
的值.
(2)已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若正实数![]() 满足
满足![]() ,且
,且![]() 对任意的正实数
对任意的正实数![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为![]() ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com