
科目: 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长度为8,
的长度为8, ![]() 的中点到
的中点到![]() 轴的距离为3.
轴的距离为3.
(1)求抛物线的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为6,且抛物线交于
轴上的截距为6,且抛物线交于![]() 两点,连结
两点,连结![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知图①②都是表示输出所有立方小于1 000的正整数的程序框图,则图中应分别补充的条件为( )
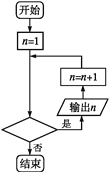
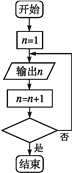
① ②
A. ①n3≥1 000? ②n3<1 000?
B. ①n3≤1 000? ②n3≥1 000?
C. ①n3<1 000? ②n3≥1 000?
D. ①n3<1 000? ②n3<1 000?
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为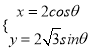 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,与直角坐标系
轴的正半轴为极轴,与直角坐标系![]() 取相同的单位长度建立极坐标系,曲线
取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)化曲线![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线![]() 与
与![]() 轴的一个交点的坐标为
轴的一个交点的坐标为![]() ,经过点
,经过点![]() 作斜率为1的直线,
作斜率为1的直线, ![]() 交曲线
交曲线![]() 于
于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
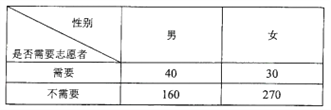
(Ⅰ)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(Ⅱ)能否有![]() 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提供更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
附: 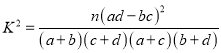
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
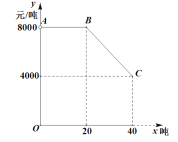
【题目】乔经理到老陈的果园里一次性采购一种水果,他俩商定:乔经理的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图像如图中的折线段
(吨)之间函数关系的图像如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() 但包含端点
但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知老陈种植水果的成本是2800元/吨,那么乔经理的采购量为多少时,老陈在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知指数函数![]()
(1)函数![]() 过定点
过定点![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() ,使得(2)中关于
,使得(2)中关于![]() 的函数
的函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com